Forces in Fluids

There are many forces that act on solids, but there are only four main forces present in fluids:

• Gravity – this is always present, but is sometimes negligible in comparison to other forces

• Pressure – this is also always present, and is always modelled as compressive and normal to the surface

• Viscous – this is always present as well, and similar to gravity, can sometimes be ignored

• Surface Tension – this is only present where a liquid meets another medium, like in bubbles and sprays

Since fluids are constantly moving, the forces surrounding them are constantly changing. We split these forces into two types: body forces and surface forces.

Body Forces

Body forces are forces that act everywhere throughout the body. They occur when a body is subjected to an external field, and the magnitude of such forces depends on the volume of the body.

Gravity is a body force

The gravitational force per unit volume is given by:

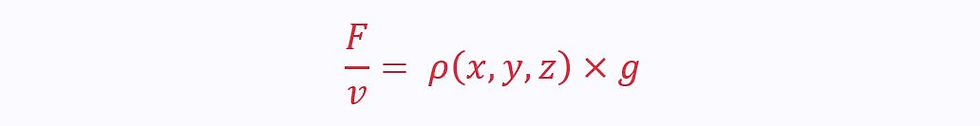
Therefore, the magnitude of the force acting on an element of volume δV (from the continuum assumption) is given by:

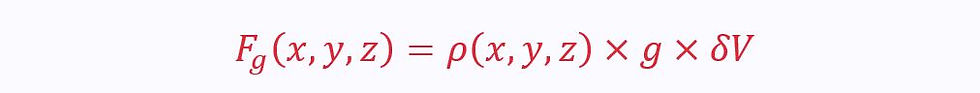
Since acceleration due to gravity is constant, the gravitational force depends only on density and volume.

Surface Force

As the name suggests, a surface force is distributed across a surface, and (just like body forces) we use it in terms of intensity: the force per unit area. You may recognise this as pressure or stress – it is the same.

If the force is evenly distributed across the surface, the stress on the surface, τ, is given by:

However, when the force is not evenly distributed, we apply the continuum assumption to a small section of the surface, δA:

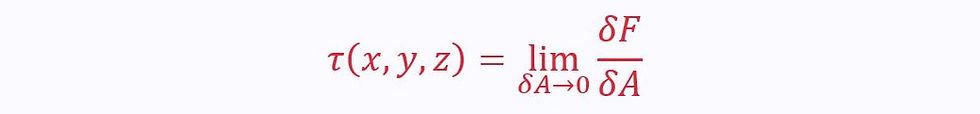
If the force is not normal to the surface, you need to find the perpendicular and parallel components: the normal and shear stresses respectively

Pressure Force

The pressure force is a surface force that is perpendicular to the surface. This means it is a normal stress:

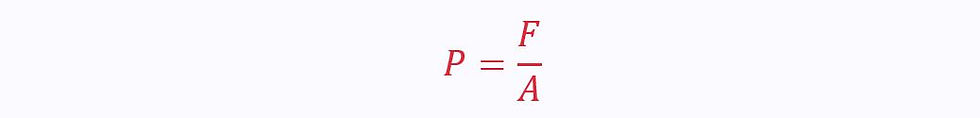
From the molecular viewpoint, pressure is caused by the molecules colliding with the surface. From the continuum viewpoint, pressure is given as the normal force per unit area on an infinitely small surface.

Pressure is always compressive, and has the same magnitude in all directions

Viscous Force

The viscous force is the frictional force that opposes a fluid’s flow. Therefore, it is a shear force, as it is tangential to the velocity. From the molecular viewpoint, it is caused by the intermolecular forces and collisions, but we look at it as deformation instead.

The viscous force is only present when the fluid is in motion.

Once the external shear force causing the fluid to move is removed, the viscous force will bring the fluid to a halt. Therefore, the viscous force dissipates energy.

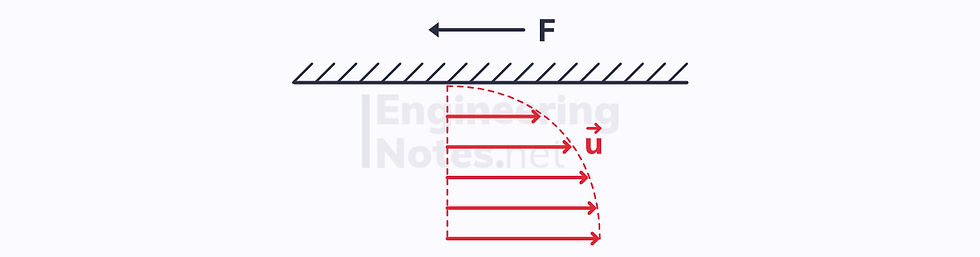
The No-Slip Condition

From velocity fields, we know that the deformation in fluids is different in different layers of the fluid:

• the layer that is furthest from a wall has the highest velocity relative to the wall

• the layer that is touching the wall has zero velocity relative to the wall

This is known as the no-slip condition.

Newton’s Law of Viscosity

Newton’s Law of Viscosity states that viscous stress is proportional to the local viscosity, the velocity gradient:

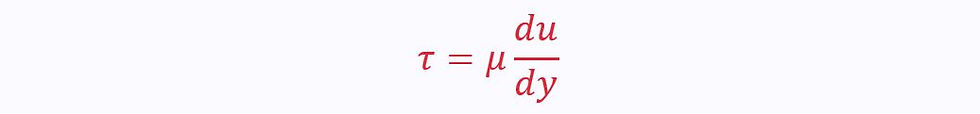
τ is still the shear stress, and μ is the viscosity.

Newton’s Law of Viscosity only applies to Newtonian Fluids.

Viscosity is different for all fluids, and depends on the conditions of the fluid, especially temperature. It is found from data tables.

Sometimes, Kinematic Viscosity, ν, is used instead of viscosity. This is defined in terms of density:

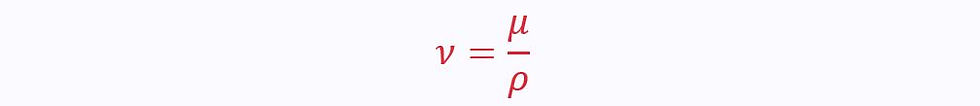
Fluids that do not obey this law are called non-Newtonian:

• Pseudoplastics are an example, in which the viscosity decreases with strain rate. A common example is non-drip paint.

• Dilatants are the precise opposite of Newtonian fluids: their viscosity increases with strain rate. The best example is corn flour & water: the harder you stir, the more solid it becomes.

• Bingham plastics behave as a solid up to a specific yield stress. Beyond this, they act as a Newtonian fluid (e.g. toothpaste)

The magnitude of the viscous force is given by the shear stress multiplied by the area:

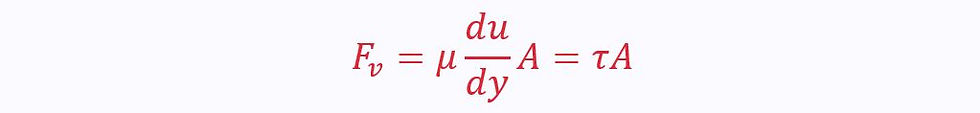
The sign of the force depends on what else is going on:

This diagram shows three layers of the same fluid.

• The darker the layer, the higher the velocity of the fluid

To know the directions of the viscous force on the top and bottom boundaries of the central layer:

• Draw the axes that are normal to the boundary between the layers, pointing outwards (y-axis)

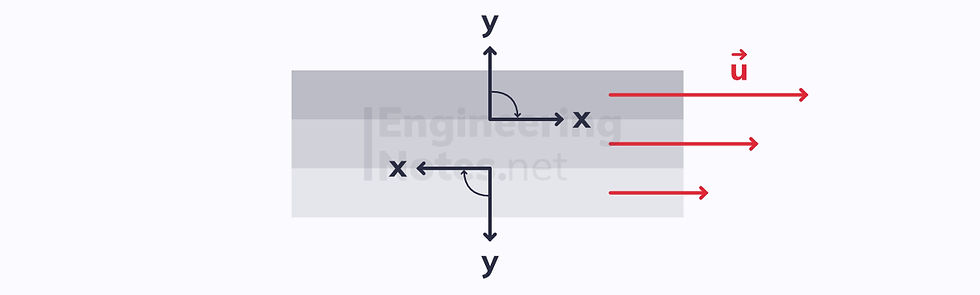
• Draw the axes that are tangential to the boundary, pointing 90 degrees clockwise from the normal boundary(x-axis)

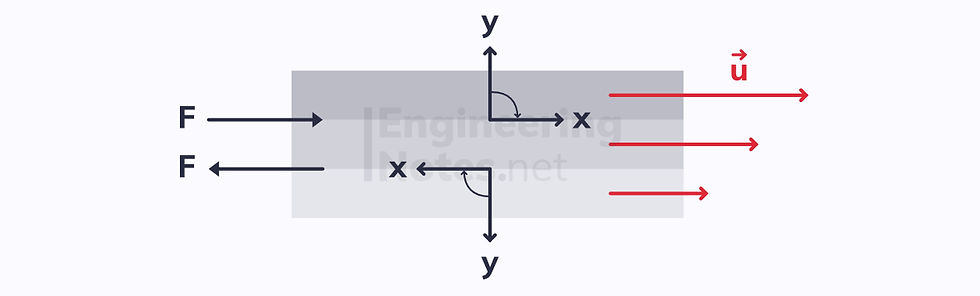
• If the tangential axis (x-axis) is in the same direction as the velocity (u), then the viscous force will be positive:

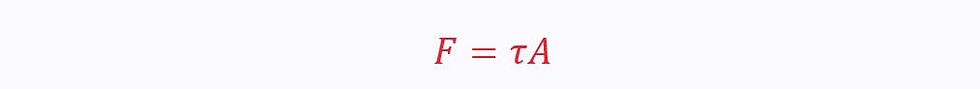
• If it points in the opposite direction, the viscous force will be negative:

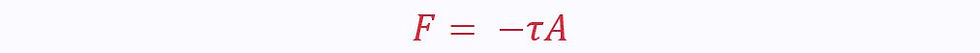
In this example, the force on the top boundary is positive, and on the bottom boundary it is negative.

Rates of deformation and velocity

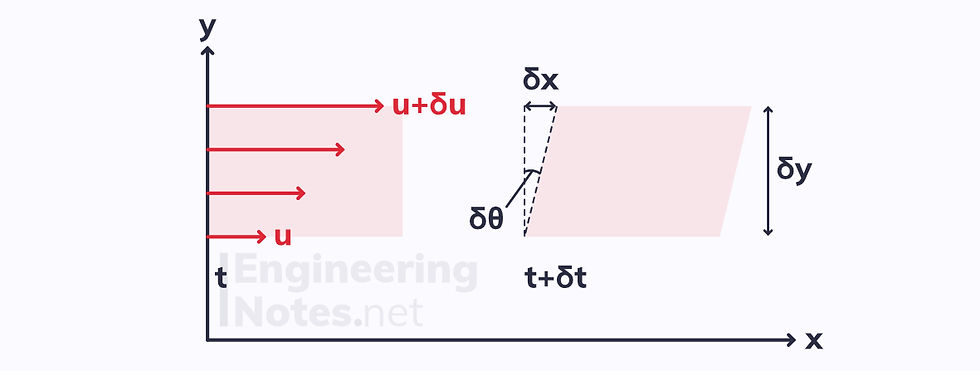
As a fluid element moves and deforms under the shear stress over a time interval δt, an angle forms between the two sides of the element, δθ. This angle is the shear strain.

For small sear strains, we can apply the small-angle approximation for tan:

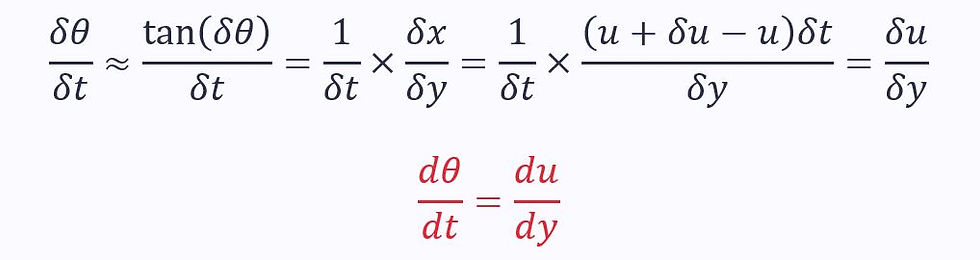
The rate of deformation (shear strain) is equal to the velocity gradient, acceleration.

Surface Tension

Surface tension is a force that occurs whenever there is an interface between a liquid and another medium and opposes the increase in contact area between the two mediums.

It happens because there is a difference in the intermolecular forces in the liquid and the other medium, meaning that liquid molecules at the boundary experience different forces than the molecules far from the boundary.

Surface tension is responsible for the shape of water droplets and bubbles.

Types of Flow

There are a number of standard types of flow to be aware of:

• Steady flow moves at a constant rate (no acceleration)

• Unsteady flow moves at a rate that varies with time

• Viscous flow is affected by viscous forces

• Inviscid flow is not affected/negligibly affected by viscous forces

• Incompressible flow has constant density (assumed for most liquids)

• Compressible flow has density that varies significantly with pressure (e.g. high-speed gasses)

• Laminar flow is ordered: there is only one space/time scale (one velocity profile)

• Turbulent flow is chaotic: there are multiple space/time scales (multiple velocity profiles)

• Internal flow is entirely enclosed within boundaries (e.g. pipes or bottles)

• External flow is unbounded (e.g. air flow around an object)

---

Summary

• Body forces in fluids (such as gravity) act everywhere in the fluid

• Surface forces act at the interfaces between fluid layers and fluid boundaries

• The viscous force is the frictional force that opposes flow, and obeys the no-slip condition

• Newton’s law of viscosity applies to all Newtonian fluids: τ = μ du/dy

• The rate of deformation is equal to the velocity gradient

• Surface tension is the force that opposes the increase in contact area between a liquid and another medium

---

Next: Fluid Statics ▸