Elasticity & Collisions

According to Hooke's Law, tension, T, is directly proportional to extension, x, in elastic strings and springs:

T = kx

The constant of proportionality, k, depends on two things: the modulus of elasticity, λ, of the material, and its unstretched, natural length, l:

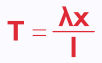
• Note: natural length is noted with a lowercase 'L' - do not confuse this with an uppercase 'i'. The font of these note sheets is not massively helpful here, so sorry!

Tension, T, is a force so is measured in Newtons. Extension and length are both distances, measured in metres. This gives the modulus of elasticity must also be measured in Newtons.

Strings can be compressed as well as stretched. In this instance, Hooke's law still applies but the force in the spring, thrust (helpfully also written as T), acts the other way.

Modelling

For all questions, strings and springs are modelled as light. This means you do not take into account its weight. See the notes sheet on modelling in mechanics for single maths - the same rules apply.

Elastic Potential Energy

When an elastic string or spring is stretched or compressed, it stores elastic potential energy within it. This is equal to the work done in stretching/compressing the string/spring.

The work done is represented by the area under a force-extension graph:

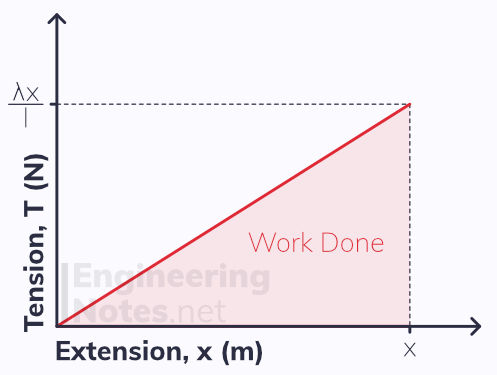
Using the equation for the area of a right-angled triangle, A = ½ab, we can find the equation for the elastic potential energy stored in an elastic system:

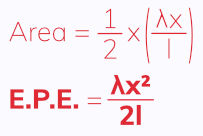
Worked Example

Elastic Collisions in One Dimension

Newton's law of restitution is used to solve problems where two particles collide directly:

Direct impact means the the particles are moving along the same straight line when they collide. This means the collision is "head-on", so to speak.

Newton's law of restitution depends on the coefficient of restitution, e, between the two colliding objects:

• 0 ≤ e ≤ 1

• In a perfectly elastic collision, e = 1, so the two particles rebound at the same speeds

• In a perfectly inelastic collision, e = 0, so the particles coalesce (join together)

When there are two unknowns in a problem, you can use the principle of conservation of linear momentum to solve simultaneously:

Collisions with a Wall

When a particle collides with a wall, the same principles apply. The only difference is, the wall does not move. Therefore, Newton's law of restitution is just taken as:

Kinetic Energy

The definition of a perfectly elastic collision (when e = 1) is a collision in which both momentum and kinetic energy are conserved. When e ≠ 1, the collision is not perfectly elastic, so some kinetic energy is lost.

This can be calculated easily once you know the masses of each particle and their initial and final speeds:

When an object collides with a wall, only the object experiences a change in kinetic energy

Oblique Collisions of Spheres with Surfaces

An oblique impact is when the collision does not act normally to the surfaces:

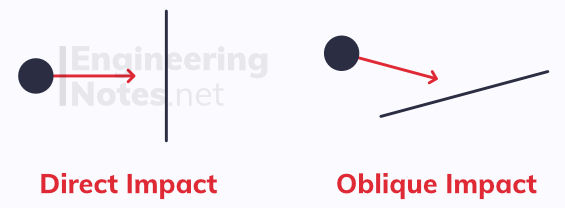
While the collision may not be perpendicular to the surface, the impulse of the particle acts perpendicular to the surface.

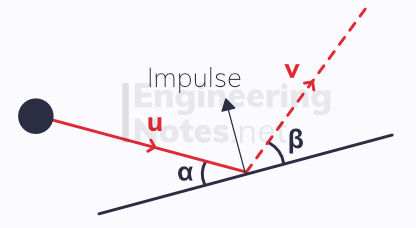
This means that the component of the velocity of the particle that acts parallel to the surface remains unchanged.

v cos(β) = u cos(α)

The components perpendicular to the surface are parallel to the impulse. Therefore, we can apply Newton's law of restitution:

v sin(β) = eu sin(α)

• e is still the coefficient of restitution between the particle and the wall

Dividing the second equation by the first eliminates u and v, leaving only the angles and e:

tan(β) = e tan(α)

Using sin² + cos² = 1 we can eliminate the angles to leave only u and v:

Angle of Deflection

The angle of deflection is the total angle through which the path of the particle changes. It is given by α + β

Vectors

Sometimes, the velocities will be given as vectors. If the surface is parallel to one of the unit vectors, this makes the question easier.

To determine the angle of deflection, θ, if the velocities before and after are given as vectors u and v respectively, use the scalar product, u . v = |u| |v| cos(θ)

Oblique Collisions of Spheres with Spheres

In addition to collisions between spheres and surfaces, you need to be able to solve problems where two spheres collide in two dimensions:

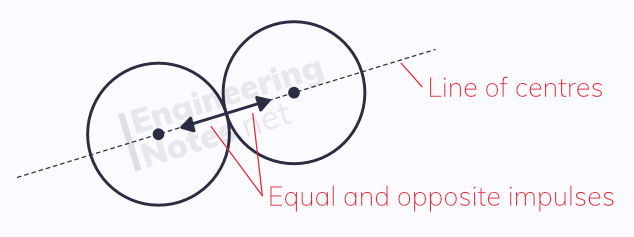
The impulse on each sphere acts along the line of centres of the two spheres

Like with oblique collisions between spheres and surfaces:

• the component of the velocities perpendicular to the impulse is unchanged through the impact

• Newton's Law of restitution applies to the parallel components of the velocities

• the principle of conservation of momentum applies parallel to the line of centres