Fluid Statics

Since fluids are almost always in motion, there is not all that much to fluid statics. Yay!

Really, the only bits are the hydrostatic equation (which is used as the basis of any fluid statics problem), pressure variation with depth, and forces on submerged surfaces – though these can be tricky.

The Hydrostatic Equation

The derivation of this equation is simple.

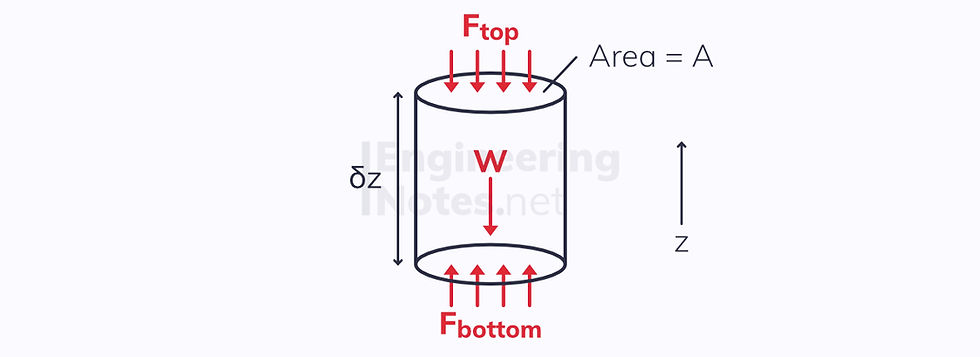
• Take a fluid particle, where the area at the top and bottom is A and the height is δz

• Taking the pressure at the bottom as P, we can work out the pressure at the top as P + the difference in pressure:

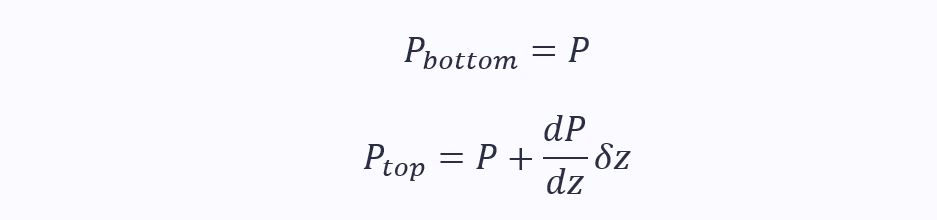
• Using F = PA, calculate the force on the bottom and top:

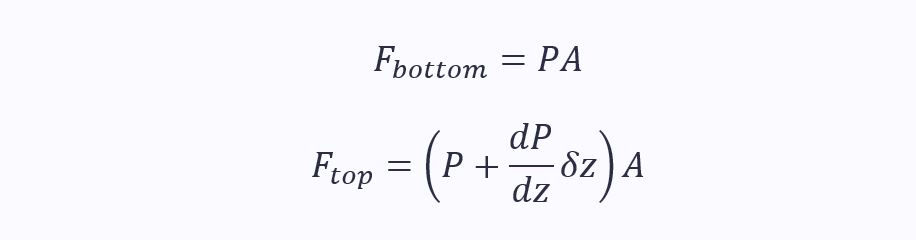
• The gravitational force of the fluid particle (the weight) is given as:

• Now, we can balance the forces on the fluid particle:

This is the Hydrostatic Equation, and integrating both sides gives the equation for change in pressure with change in height that you are probably familiar with:

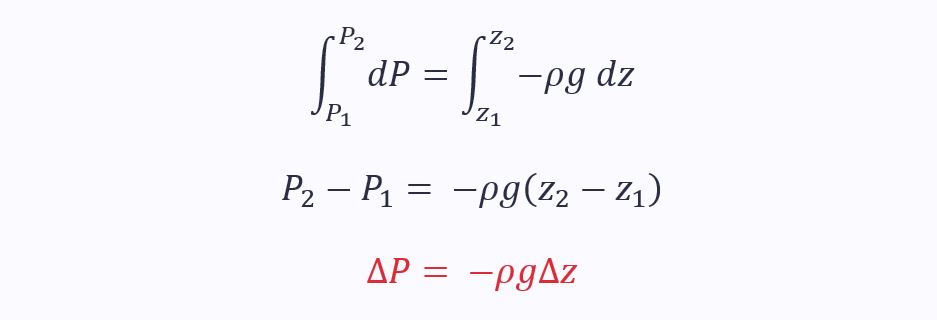
Note that you are probably familiar with ΔP = ρgh. This is the same, h is just defined as (z₁-z₂), hence the negative sign disappears. This form is sometimes known as the integrated form.

It is important to note that in this derivation, density has been assumed to be constant. In reality, this is often not the case.

Gauge Pressure

In the derivation above, we have ignored atmospheric pressure. This is because we assume it acts the same on each surface, so cancels out.

Pressure that ignores atmospheric pressure is called gauge pressure, as it is the pressure a gauge will read (for example on a bicycle pump).

Manometry

A manometer is a device used to measure a pressure difference:

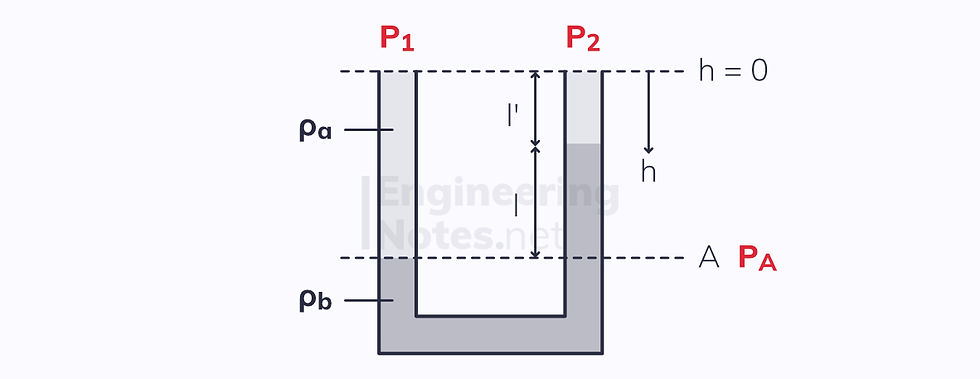
If we know the difference in heights of the fluid interfaces, l, we can calculate the pressure difference of P₁ and P₂, because the pressure at A (a point in height that we chose to define) must be the same in each side:

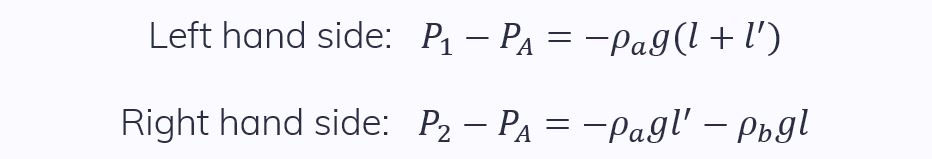
Combining these equations gives:

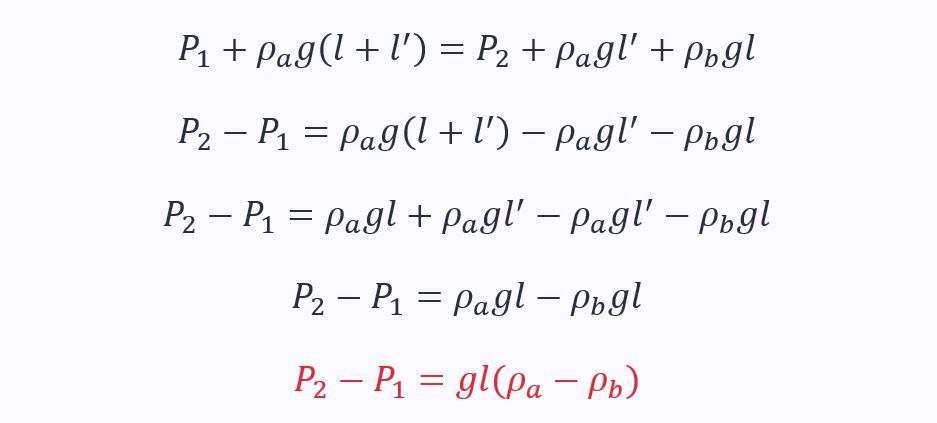
As you can see, the height l’ is irrelevant.

Hydrostatic Forces on Flat Surfaces

Since pressure varies with depth, the magnitude of the force on a submerged surface also varies with depth: it is known as a distributed force.

When combining fluid mechanics with solid mechanics, however, this is not helpful. Instead, we want to know the resultant force of the pressure on the surface. There are three things we need to know to fully define the resultant force:

1. The magnitude

2. The point of application

3. The direction

The direction is easy: pressure force always acts perpendicular to the surface. To find the magnitude and direction we use a particular form of two-dimensional integration: surface integrals.

We know that the pressure force on an infinitesimally small area is given by:

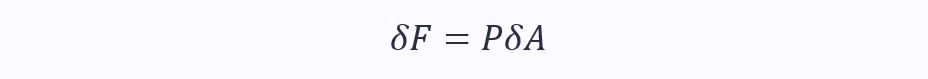
Integrating this on a surface gives the sum of the forces on the infinitesimally small areas:

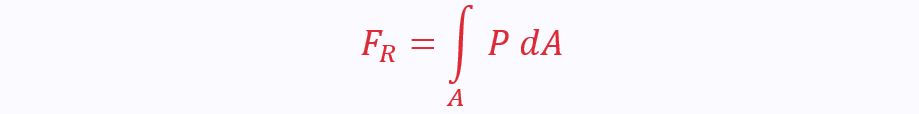
The subscript A under the integral sign tells us it is a surface integral.

Solving Surface Integrals

Writing pressure in terms of y (using the hydrostatic equation) gives:

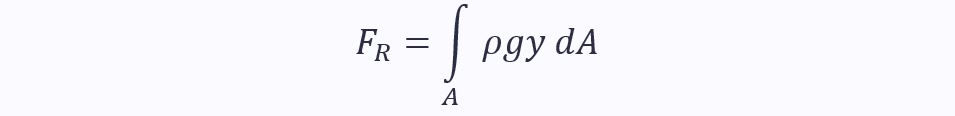
Converting this into a function involving dy allows us to integrate the function as a standard integral:

• For a rectangle width y and length L, dA can be written as L dy:

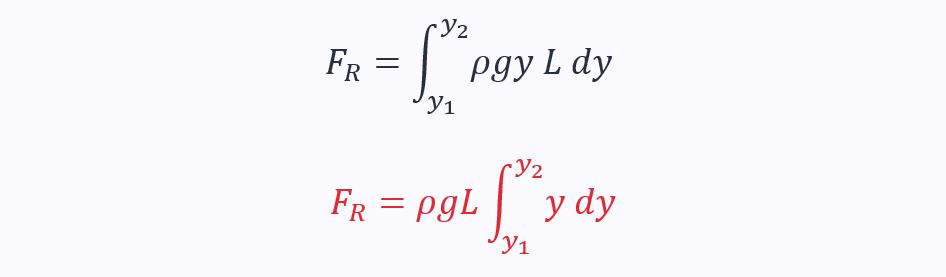
You must find pressure as a function of y. It is easy to forget to do this!

Finding the Point of Application

To find the point at which the resultant force acts, you can solve using moments, as the resultant force must have the same moment as the sum of all the forces acting on the infinitesimally small areas.

y’ is the distance along the surface that the resultant force acts on.

The sum of moments of the tiny forces can be worked out by another surface integral, but this time, there is an extra y term. Therefore, the moment is given by:

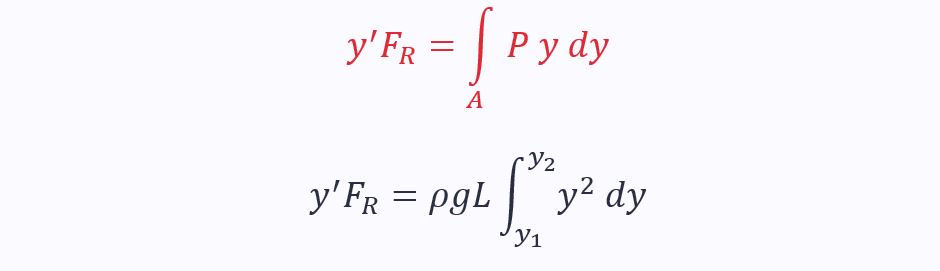
This means that the distance along the surface that the force acts on, y’, is given by:

Now that we know all three parts of the resultant force (magnitude, point of application and direction), we can solve problems like a vertical gate on the side of a tank:

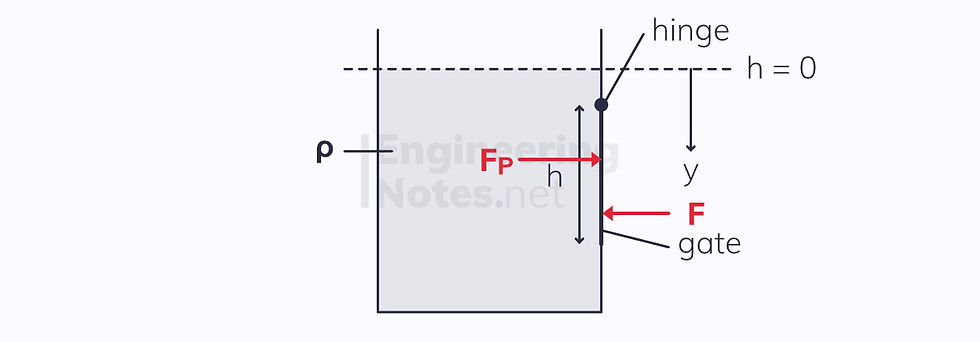
If you know the dimensions and depth of the gate, as well as the density of the fluid in the tank, you can work out where and what magnitude of force is required on the outside of the gate to keep it closed.

Hydrostatic Forces on Curved Surfaces

Integrating pressure over a curved surface is often very complicated. Instead, there is a simpler method that involves balancing horizontal and vertical forces.

Take this quarter-cylindrical surface:

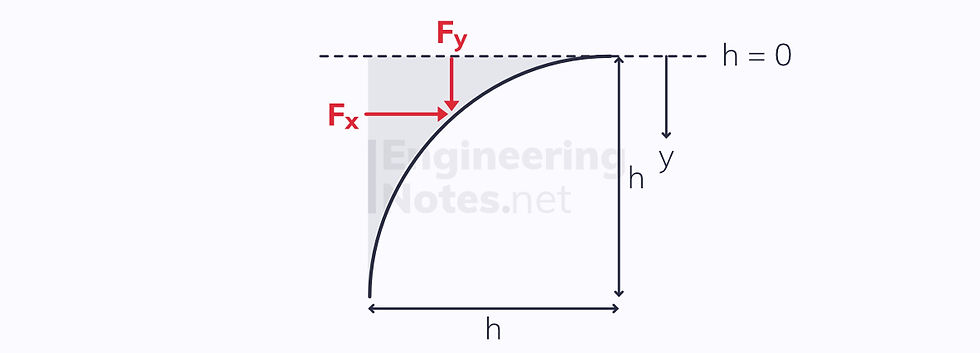
• The horizontal force acting on it is the resultant pressure force and is found exactly the same as for a flat vertical surface:

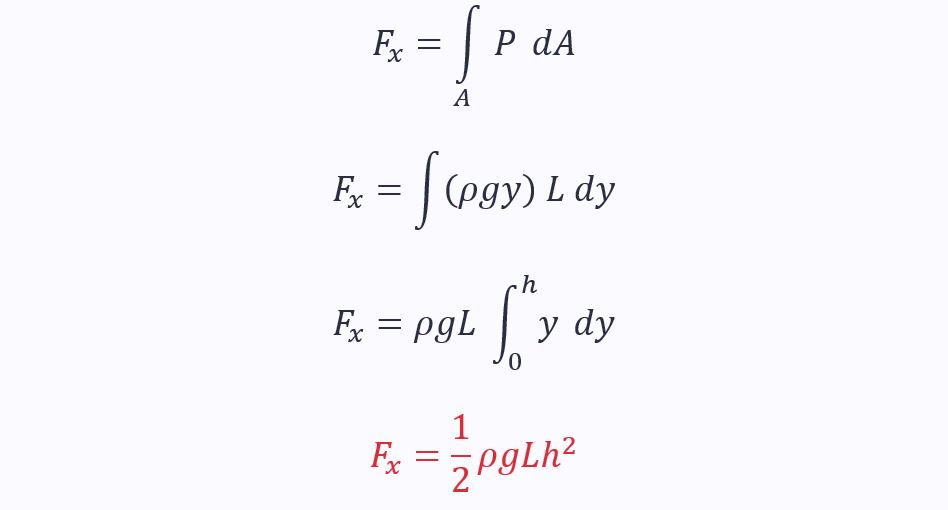
• The vertical force action on the surface is the weight of the fluid above, acting downwards:

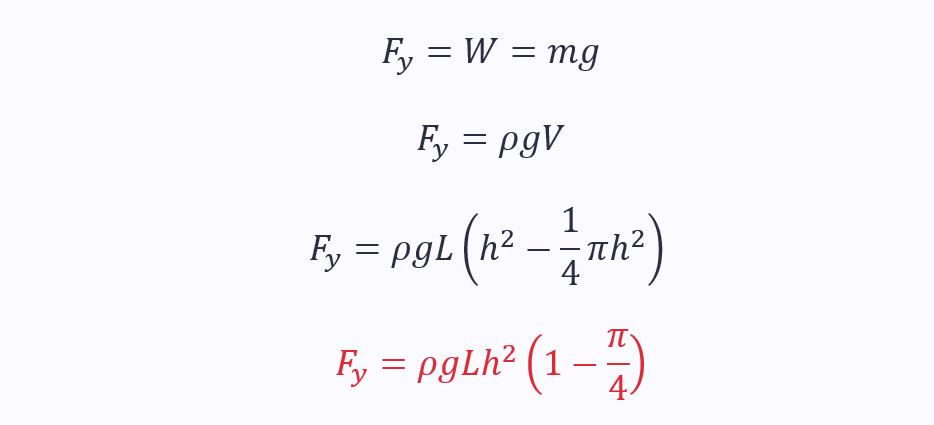
Therefore, the total resultant force is given as a vector:

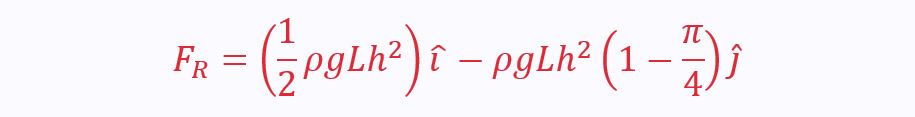
The j component is negative, as the weight acts downwards.

Buoyancy

All submerged bodies experience an upwards force. This is because the pressure force acting up on their lower surface is greater than the pressure force acting down on their upper surface. The difference in force is known as upthrust, or the buoyancy force.

According to Archimedes’ Principle:

The magnitude of the upthrust is equal to the weight of water displaced.

This is proven hydrostatically:

If the weight of the object is less than or equal to the magnitude of the upthrust, the object will float.

If the centre of gravity of the object does not align with that of the displaced fluid, there will be a net resultant moment acting on the object.

• This is what causes ships to capsize.

---

Summary

• The change in pressure with height is given by the hydrostatic equation: Δp = ρgΔh

• Gauge pressure neglects atmospheric pressure, as it acts the same everywhere

• A manometer is used to measure a difference in pressure

• Surface integration is used to find the resultant force and moment on submerged surfaces

• If the surface is curved, split the resultant force into vertical and horizontal components where the vertical component is the weight of water above

• Archimedes’ Principle states that the magnitude of the upthrust (buoyancy force) is equal to the weight of water displaced

---

Next: Control Volume Analysis ▸