The Bernoulli Equation
In this notes sheet...
The Bernoulli Equation
Generally, the Bernoulli Equation is expressed between two points, 1 and 2:
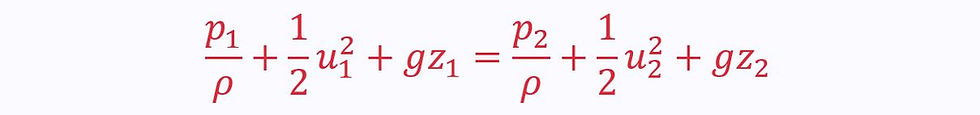
See the derivation of the Bernoulli Equation here.
This applies to steady, inviscid flow with constant density, where the two point lie on the same streamline, or the Bernoulli constant of each is the same:
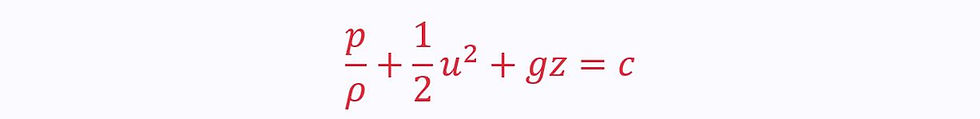
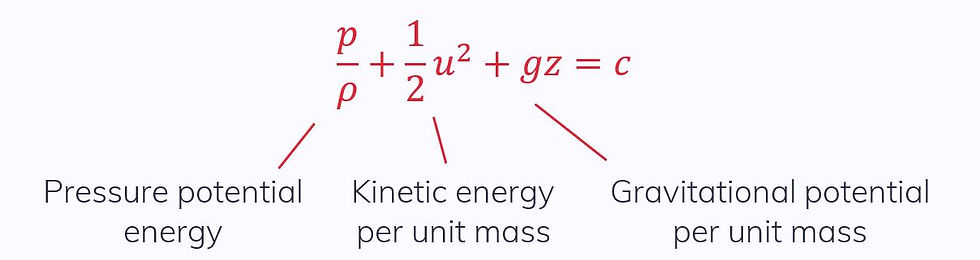
We can use the Bernoulli equation to model the conservation of mechanical energy (when there is no friction).
Stagnation Point Flow
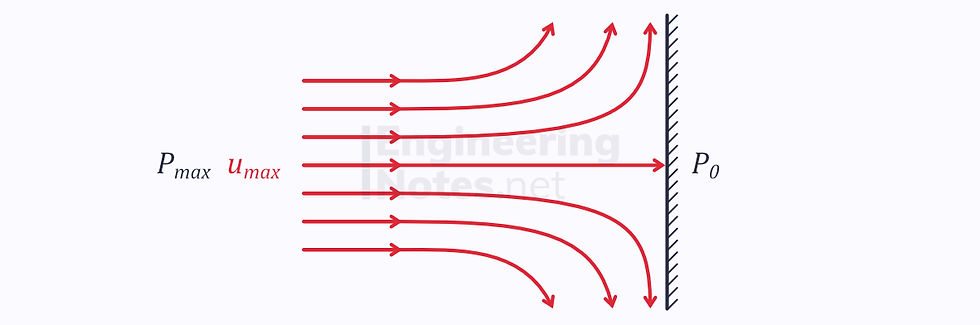
In an ideal situation, when inviscid, incompressible steady flow with uniform velocity and pressure hits a wall, the central streamline will not deflect but become stationary.
This is known as the stagnation point.
In this instance, the Bernoulli equation simplifies to:
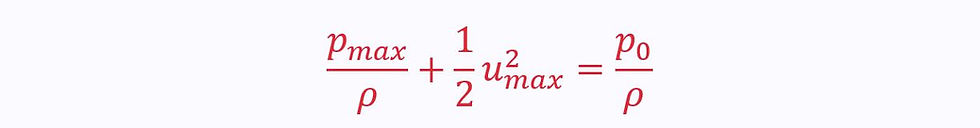
All the mechanical energy is in terms of pressure potential energy: the maximum possible pressure in a given flow (stagnation pressure).
In reality, this does not occur, as close to the wall the fluid is acted upon by the viscous force.
Conservation of Energy for Steady Flow
The first law of thermodynamics is the conservation of energy in a system:
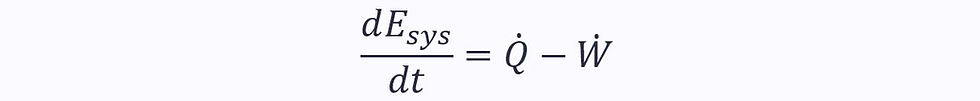
We can substitute this into the Reynolds transport theorem, where η is the total energy per unit mass:
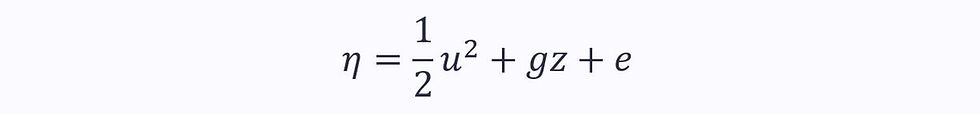
And for steady flow, where the d/dt term disappears:
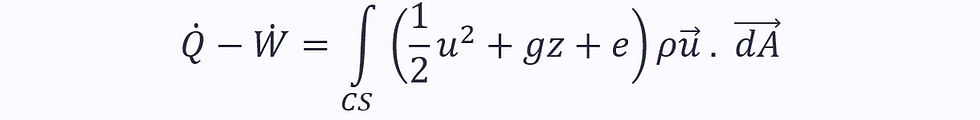
Here, the work done by the pressure force is included in the work term on the left. This is not helpful to us, so we want to extract it.
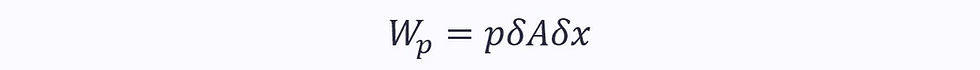
Therefore:
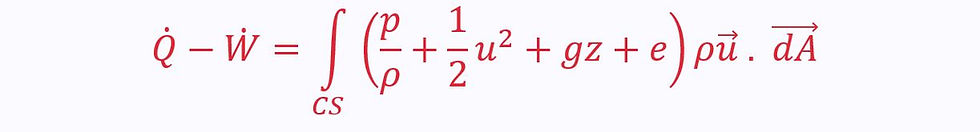
The shaft work on the left does not include pressure work (this is in the integral on the right).
For a simple control volume with one inlet and one outlet, the bernoulli equation becomes:
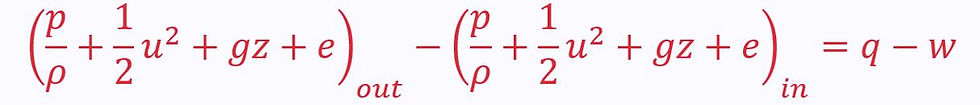
The Pipe Flow Energy Equation
This is a simple conservation of energy equation for adiabatic flow. This means that the Q term disappears - though there is still a small amount of heat lost through friction. Therefore, we take into account energy losses:
The pipe flow energy equation thus becomes becomes:
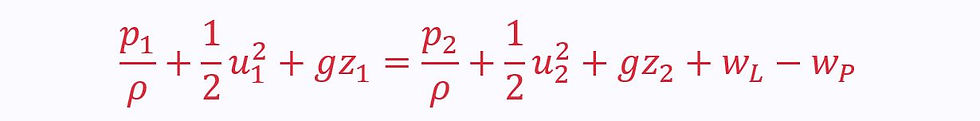
Often, it is more helpful to give values in terms of height – from this the pressure can easily be calculated. We call these ‘heads’, and so the lost work and pump work become lost head and pump head respectively:
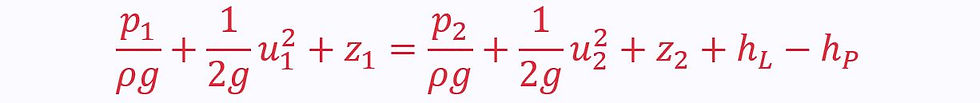
This only applies in steady, adiabatic, incompressible, uniform velocity flow between a single inlet and outlet
As you can see then, it’s a pretty niche equation.
The pipe flow energy equation is the adiabatic equivalent of the SFEE in thermodynamics but for incompressible fluids, not compressible gasses.
Comments