Further Integration
- A-Level Further Maths

- Sep 18, 2020
- 3 min read
Updated: Dec 7, 2020
This is a bit of an odd notes sheet - its just an amalgamation of all that extra integration stuff:
improper integrals
the mean value of a function
inverse trig
partial fractions
volumes of revolution
Improper Integrals
In single maths, you learn how to integrate to find the area enclosed between a curve and the x-axis between two fixed limits. An improper integral is when one or both limits are infinite, or when the function is undefined at a certain point in the given interval.
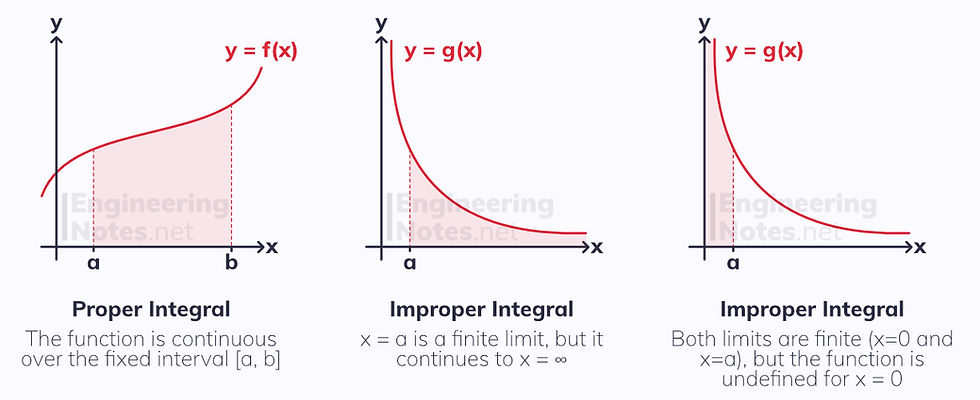
An improper integral does not always exist: if it does, it is convergent; if it does not, it is divergent.
One Infinite/Undefined Limit
To see if an improper integral with one infinite and one finite limit is convergent you need to substitute the infinite limit for t, and consider what happens as the function tends towards infinity:
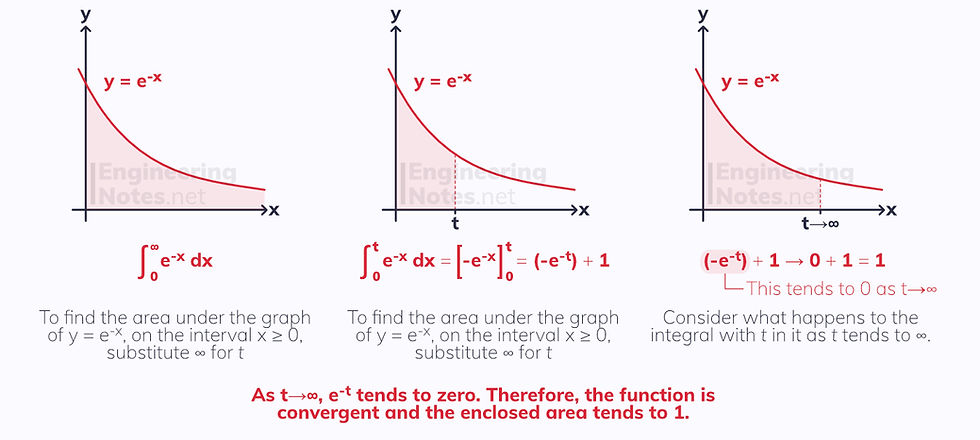
If the integral part with t in it did not tend to 0, but instead tended to ∞, the function would be divergent.
Two Infinite/Undefined Limits
When both limits are infinite or undefined, you need to separate the integral into two improper integrals each with one infinite and one finite limit.
The finite limit of both parts must be the same.
It is generally good to use a simple value such as x=0, as this makes workings a lot simpler.

Even if only one of the two separated integrals does not converge, the whole integral will not converge to a defined value.
Mean Value of a Function
It is possible to find an average for the area enclosed under a graph over a fixed interval. The height of this average area is known as the mean value of the function:
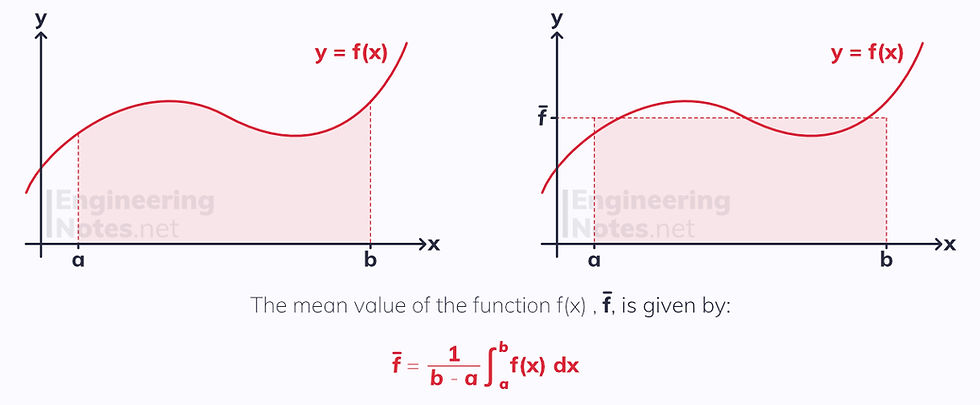
The mean can be transformed along with the graph it represents:

Inverse Trigonometric Functions
It is possible to differentiate inverse trigonometric functions implicitly. This leads to standard results that are incredibly useful for both differentiation and integration:
Differentiating Inverse Trigonometric Functions
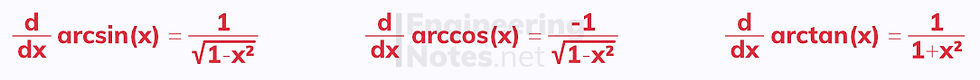
It is possible to derive these differentiation functions by differentiating implicitly.
Integrating Inverse Trigonometric Functions

It is possible to derive the function for the second integral by substitution.
Integrating with Partial Fractions
If the denominator of a partial fraction has a square x-term in it, you cannot use the standard method to find the numerator coefficients. Instead, you must write the coefficient of the partial fraction with a quadratic denominator as a linear function in x:

These partial fractions can then often be integrated using the inverse trig results above.
Volumes of Revolution
The mathematical equivalent of pottery, integration can be used to find volumes of circular shapes, where the sides are defined by equations of lines integrated for a full rotation about a coordinate axis.

For example, the line y=r, where r is a positive integer, becomes a cylinder of radius r when revolved about the x-axis.
About the x-axis
To calculate the volume of revolution for any function y = f(x) that is rotated 2π radians about the x-axis between x=a and x=b, use the formula:

About the y-axis
To calculate the volume of revolution for any function y = f(x) that is rotated 2π radians about the y-axis between y=a and y=b, use the formula:

Adding and Subtracting Volumes
Often, for hollow object or complex shapes, you will need to subtract one volume from another to find a sort of shell. Similarly, you may need to add volumes. This is exactly the same as finding the area between different curves, just in 3D.
Common examples include cones and cylinders:

A cylinder of height h and radius r has volume πr²h
A cone of height h and base radius r has volume ⅓πr²h
Parametric Volumes of Revolution
There is no need to convert parametric equations into Cartesian form to find their volumes of revolution. Instead, a variant of the chain rule can be used. This means you will need to differentiate one of the equations, depending on whether the revolution is around the x- or y-axis.
To calculate the volume of revolution for parametric equations x = f(t), y = g(t) that are rotated 2π radians about the x-axis between x=a and x=b, use the formula:
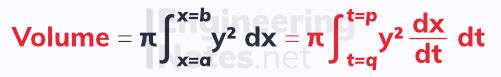
Where p and q are the values of t when x=a and x=b respectively
To calculate the volume of revolution for parametric equations x = f(t), y = g(t) that are rotated 2π radians about the y-axis between y=a and y=b, use the formula:

Where p and q are the values of t when y=a and y=b respectively



Comments