Hyperbolic Functions

Hyperbolic functions are similar to trigonometric functions, but are defined in terms of exponentials. There are three fundamental hyperbolic functions: sinh, cosh and tanh:

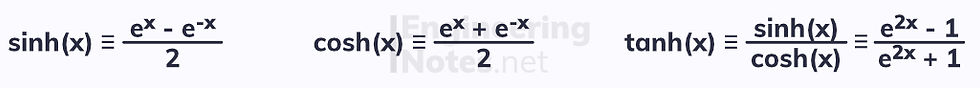
Similarly, the reciprocal of each function exists:

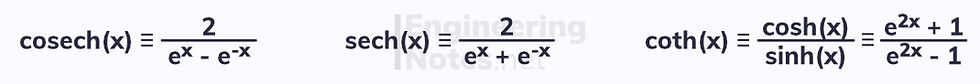
Hyperbolic Graphs

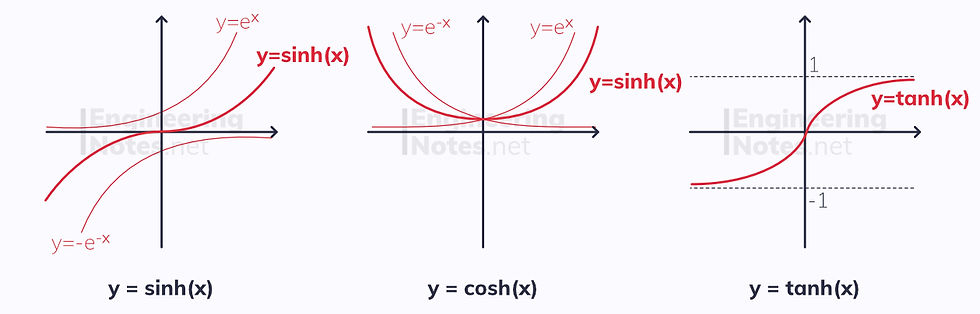
For any value of x, sinh(-x) = -sinh(x)

• y = sinh(x) has no asymptotes

For any value of x, cosh(-x) = -cosh(x)

• y = cosh(x) never goes below y=1

• y = tanh(x) has asymptotes at y = ±1, and always stays between these

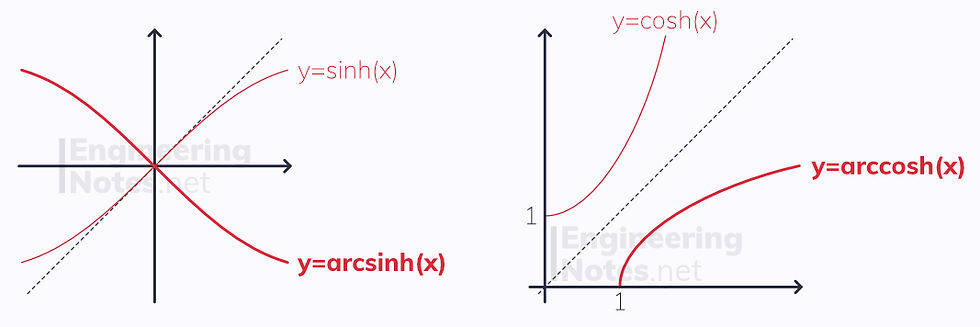
Inverse Hyperbolic Functions

Just like sin, cos and tan, the hyperbolic functions have inverses, arcsinh, arcosh and artanh:

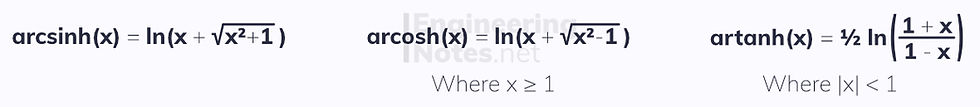
The graphs of these are their respective reflections in the line y=x:

Hyperbolic Identities & Equations

The same identities exist for hyperbolic functions as they do for trigonometric functions:

sinh(A ± B) ≡ sinh(A) cosh(B) ± cosh(A) sinh(B)

cosh(A ± B) ≡ cosh(A) cosh(B) ∓ sinh(A) sinh(B)

Equations with a sinh² in them, however, are different:

cosh²(x) - sinh²(x) ≡ 1

Note that here, the sinh² is negative (the trigonometric identity is sin² + cos² ≡ 1). This is known as Osborn's rule:

According to Osborn's rule, when using trigonometric identities as hyperbolic identities, any sinh² must be multiplied by -1.

Differentiating Hyperbolic Functions

This is very similar to trigonometric functions:

Note that the derivative of cosh(x) is positive sinh(x), not negative.

The inverse functions differentiate as such:

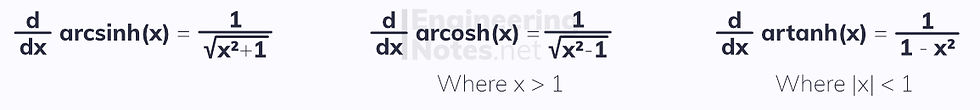
Integrating Hyperbolic Functions

Simply the reverse of differentiation, but remember the " +c " and that the signs are different:

The inverse functions can also be integrated:

These standard results for when the equation you need to integrate does not have either (x²+1) or (x²-1) in the root in the denominator: