Materials

Materials can have many different properties, and experience a number of external and internal forces. The two main such forces are the tensile and compressive forces, relating to extension (stretching) and compression (squishing) respectively.

Hooke's Law

The most common example of these forces being applied are in a helical spring: these have a natural length, and are either stretched or compressed depending on direction of force applied. The distance of this deformation is called the extension (regardless of direction) and according to Hooke's law:

Extension is directly proportional to the force applied, provided the elastic limit is not passed

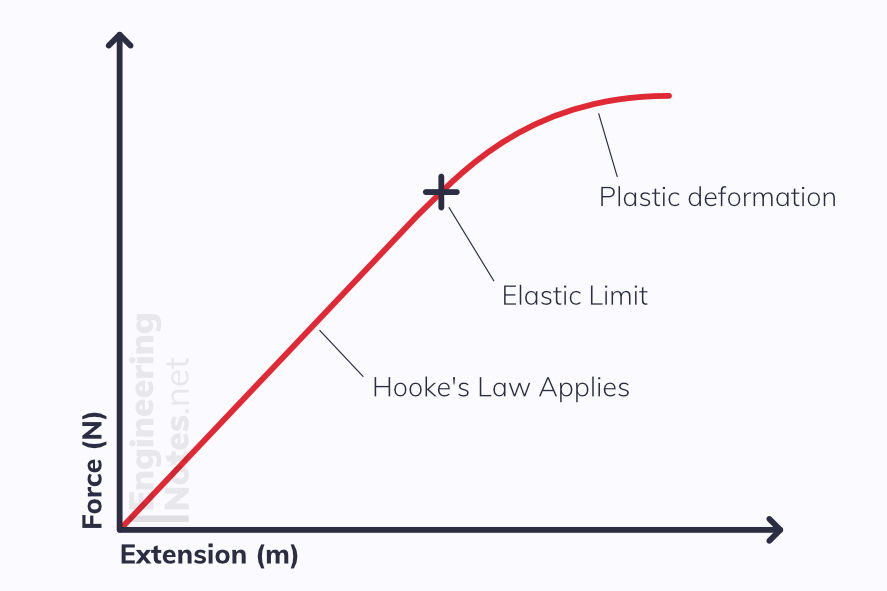
As you can see in the graph, the relationship is linear, where the gradient is the force constant up to the elastic limit - if this is exceeded, the object will no longer return to its initial shape, - plastic deformation has occurred. 

F = kx Force = force constant x extension

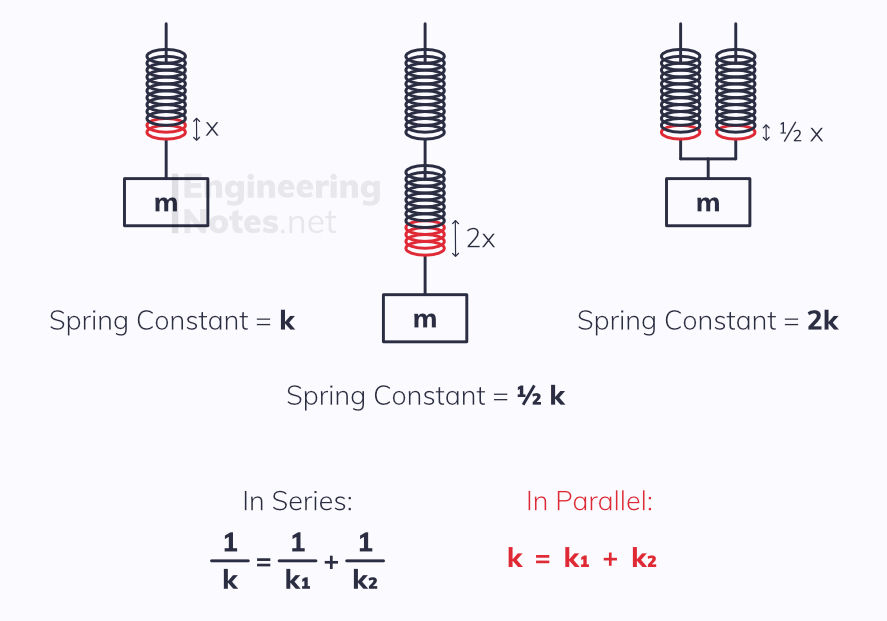
Multiple String Systems

Springs (and indeed any elastic materials) can be combined either in series or in parallel, with vastly different effects:

Elastic Potential Energy

All springs, just like any object under tensile or compressive forces, store Elastic Potential Energy. This is equivalent to the work done in extending/compressing them, and since W = Fx, this is the area under a force-extension graph.

W = 1/2 Fx E = 1/2 Fx E = 1/2 k x^2

Stress, Strain & Young Modulus

Tensile Stress

Stress is the force per unit cross-sectional area. Its units are Pascals, Pa.

σ = F/A stress = force / cross-sectional area

Tensile Strain

Strain is the fractional change in length of the material. It is a ratio, so has no units.

ε = x/L strain = extension / original length

Young Modulus

Provided the limit of proportionality is not exceeded, stress is directly proportional to strain. The constant is known as the Young Modulus, and this is a fixed property of any given material. The units are also Pa.

E = σ/ε Young Modulus = tensile stress / tensile strain

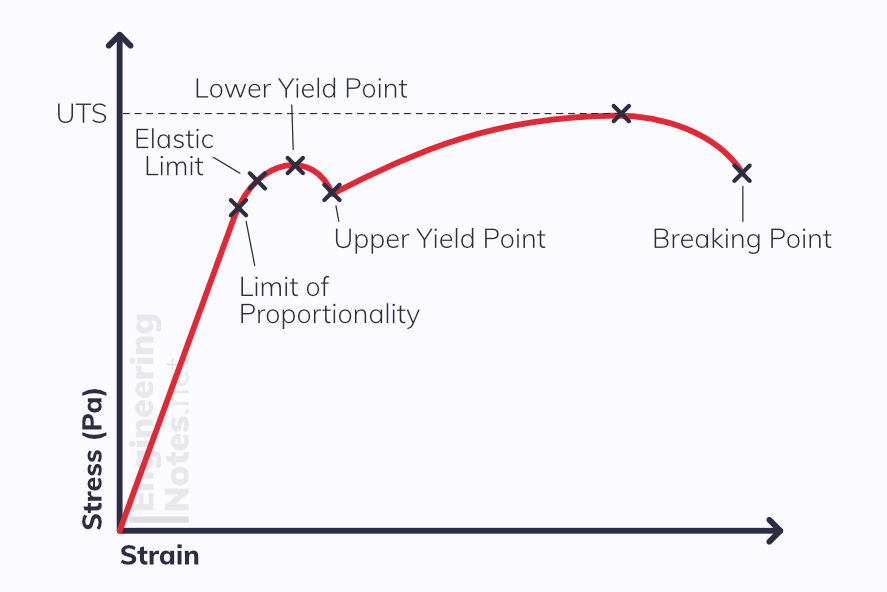
This graph shows the elastic profile of a typical metal wire, such as mild steel.

• Up until the limit of proportionality, the wire obeys Hooke's Law.

• Between the limit of proportionality and the elastic limit, the wire deforms elastically, and plastically hereon-after.

• Between the two yield points, the material extends dramatically.

• The stress increases until it reaches the UTS - the Ultimate Tensile Stress. This is the maximum stress the wire can take.

• Finally, the stress decreases until the material just breaks.

Material Properties

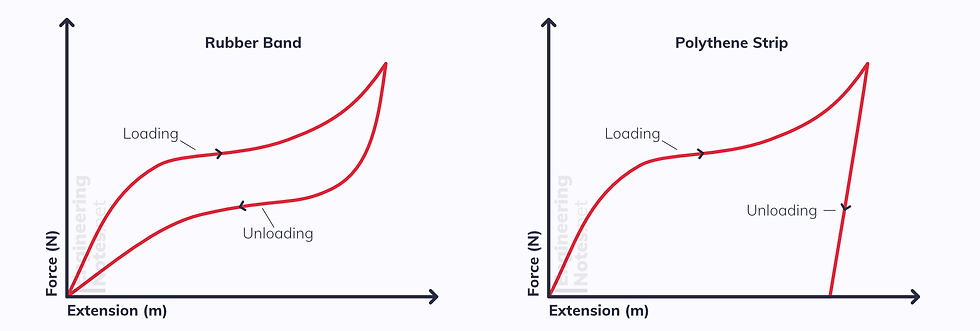
Ductile Materials curve on a stress strain graph, and even when deformed they keep their strength. See the steel graph above.

Brittle materials do not curve. To start with, the graphs are identical when they obey Hooke’s law. Then, when the stress reaches a certain point, the material snaps without deforming. 

Stronger materials can withstand more stress before they break than weaker ones.

Stiffer materials are harder to stretch or compress as they have a high young modulus.

Stiffness is not a sign of strength.

Polymeric materials have their molecules arranged in long chains, which gives a vast range of properties.

• Polythene behaves plastically, meaning applying enough stress will deform it into a new shape permanently, and it is also ductile.

• Rubber behaves elastically, but its loading and unloading graphs are different. This means less energy is released on the unloading graph, so less work is done, and some is lost as heat.