Composites
- Engineering

- Nov 19, 2020
- 3 min read
Updated: May 12, 2021
In this notes sheet...
Pure materials and alloys are good for standard applications, but often a very specific set of properties is required from a material. In this instance, a composite may be used or even designed in order to maximise the best properties of a number of materials combined.
A composite is a material that employs multiple different phases to attain better specific properties than either phase alone.
There has to be a noticeable boundary between the two phases, and one needs to be introduced to the other rather than the two phases forming simultaneously – a two-phase slow cooled metal alloy is not a composite, then.
Composites occur naturally as well as artificially. Good examples are bones and carbon fibre respectively.
Composite Structure
There are two main phases in a composite:
the continuous matrix phase is the weaker phase that transfers applied loads to the reinforcement. It also acts as protection for the reinforcement.
the dispersed reinforcement phase adds the desired property (strength, stiffness, hardness etc.) to the material by delaying crack dispersion.
The matrix could be a metal, ceramic or a polymer. The reinforcement is generally a ceramic (carbon is especially common), but could take a number of forms:
Particulate reinforced composites use small particles, like spheres or flakes.

Fibre reinforced composites contain fibres. These could be very short, fairly long, or even continuous throughout the structure.

Structural Composites may use particles, fibres, or even both for reinforcement, arranged in specific forms to maximise strength: honeycombs, layers and sheets are common.
Types of Composites
Metal Matrix Composites (MMCs)
A cermet is a ceramic-metal composite.
Typically used for cutting tools and dies.
Advantages include high elastic modulus, toughness, and ductility.
Disadvantages include the high density and expense.
Standard matrix materials include:
Aluminium & aluminium-lithium alloys
Magnesium
Copper
Titanium
Super-alloys.
Standard reinforcement materials include:
Graphite
Alumina (aluminium oxide)
Silicon carbide
Boron
Tungsten carbide
Ceramic Matrix Composites (CMCs)
Generally used for temperature and corrosion sensitive applications, like engine components and deep-sea mining, or extremely hard cutting tools.
Advantages include the excellent corrosion and temperature resistance.
Disadvantages are the extreme brittleness and expense.
Standard matrix materials include:
Silicon carbide
Silicon nitride
Aluminium oxide
Standard reinforcement materials include:
Carbon
Aluminium oxide
Polymer Matrix Composites (PMCs)
Generally used for lightweight structures, like aircraft, vehicles, sporting, and marine equipment.
Advantages include low density, easy processing, and specific properties
Disadvantages include poor temperature and chemical resistance.
Standard matrix materials include:
Nylon
Polypropylene (PP)
Epoxy
Phenolic
Polyester
Standard reinforcement materials include:
Glass
Carbon
Boron
Aramid (Kevlar)
Critical Fibre Length
The length of fibres makes a huge difference to the composite’s performance.
Too short, and the adhesive bond between the fibre and the matrix will break before the fibre itself breaks, so the fibre pulls out of the structure
Too long, and the adhesive bond between matrix and fibre transmits too much load, breaking the fibre.
As with most things, a fine balance is required between the two. This is known as the critical fibre length.
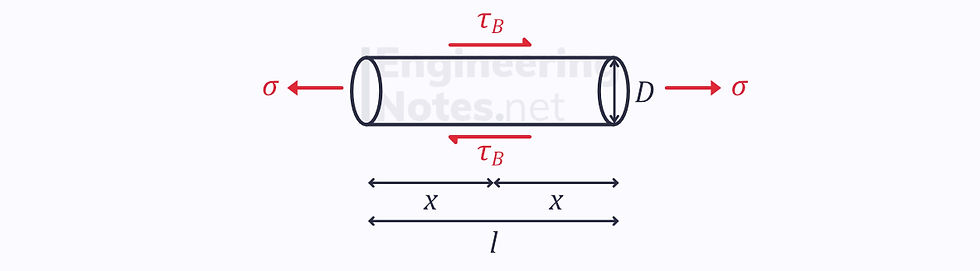
For a uniform circular cross-section fibre of half-length x, the shear force at the fibre-matrix boundary is given by:
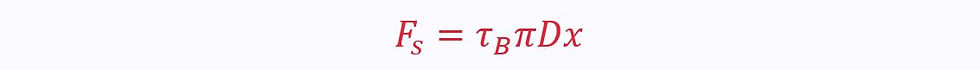
The force required to break the fibre is given by:

The critical half-length is when these two forces equal one another:
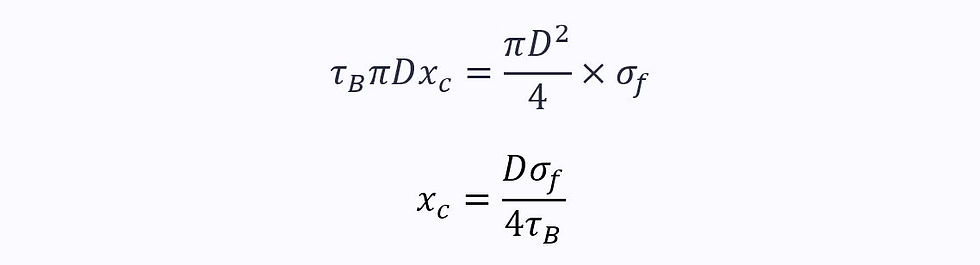
The critical length is therefore:

Standard fibre lengths are:
0.2mm for a carbon fibre in an epoxy matrix
0.5mm for a glass fibre in a polyester matrix
1.8mm for a glass fibre in a polypropylene matrix
Fibre Volume Fraction
Fibre composites are generally described in terms of fibre volume fraction: this is (you guessed it) the proportion of the materials volume that is taken up by fibres not matrix.

For fully aligned fibres, the volume fraction could be up to around 65%. Generally, it is lower.
For uniform cross-sectional and continuous fibres, the area fraction is the same as the volume fraction.
Loading Fibre Composites
Isostrain

When the fibres are parallel to the applied load, and the fibre-matrix adhesive bond does not break, the matrix and fibres experience the same strains:

The total force is therefore the sum of the forces in the fibres and matrix:

When both the fibres and the matrix are in the linear elastic region, Hooke’s law applies to both:

Therefore:
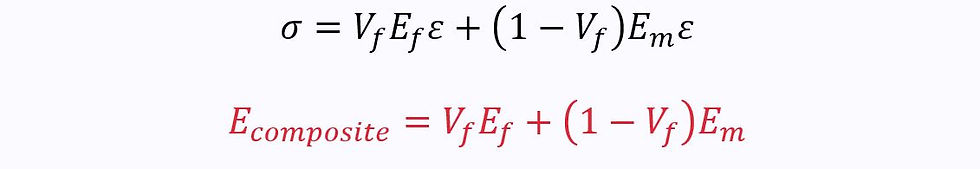
Isostress

When the fibres are perpendicular to the applied stress, the stress in the fibres and matrix are the same:
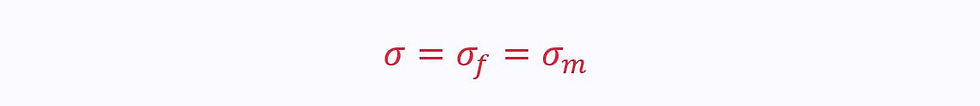
Therefore:

Comparing Isostrain and Isostress

Stress-Strain Behaviour

It is harder to predict the strength of a composite without empirical investigation, however we can predict the behaviour by assuming it will initially perform similar to the fibre, but deform uniformly once the matrix begins to undergo plastic deformation.

Comments