Defects & Deformation of Crystal Structures
- Engineering

- Nov 26, 2020
- 3 min read
Updated: Mar 1, 2021
In this notes sheet:
There are two types of deformation of crystalline materials: elastic and plastic. The former is fully reversible, whereas in the latter, atomic planes slip over one another to form a new, different formation. This kind of deformation is irreversible.

Note that the elastic deformation graph could be non-linear (e.g. rubber)
Slip & Slip Systems
The slipping of atomic planes (slip planes) happens in whatever direction requires the least energy. It is brought about by the application of an external force, resulting in shear stresses within the crystal structure.
In a perfect sample, the slip would occur over the whole plane at once, however imperfections in the crystal structure prevent this: slip is a gradual process.

Close-packed planes are the most susceptible to slip. This is because more energy is required for a non-close-packed plane to slip, as there is a greater distance for each displaced atom to move.
The number of slip systems a crystal lattice has reflects how likely slip in the structure is.
The more slip systems present, the more susceptible to slip.
This is determined as the product of close-packed directions and non-parallel close-packed planes:

Lattices with few slip systems are said to show brittle deformation, while those that have many undergo ductile deformation.
HCP Slip Systems
There are three close-packed directions per close-packed plane, however all close-packed planes are parallel. Therefore, the number of slip systems is 3, so the deformation is brittle:

FCC Slip Systems
The close-packed planes in an FCC lattice are along the diagonal-corner, and there are four:
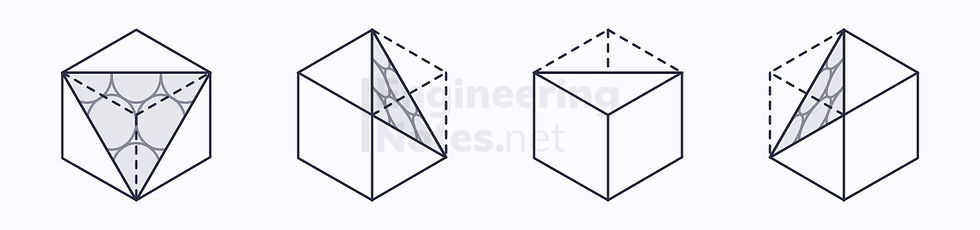
Each plane has three close-packed directions, so the number of slip systems is 12, so the deformation is ductile.
BCC Slip Systems
There are no close-packed planes, but there are 6 nearly-close-packed planes, each with two close-packed directions:
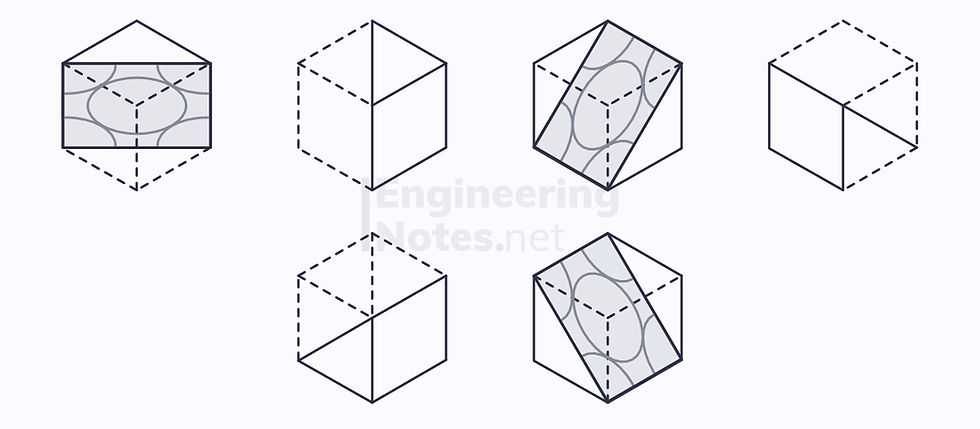
Therefore, the number of slip systems is 12, so the deformation is ductile.
Calculating Deformation
The applied stress must be resolved in terms of the slip plane, φ, and direction, λ:
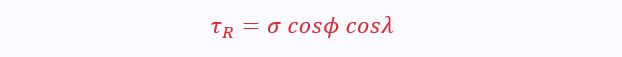
σ is the normal stress, given by F/A
Under the application of a shear stress, slip will occur in the most favourably orientated slip system. This is the system with the largest value of resolved shear stress:
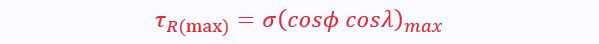
The value of shear stress required for this slip to occur in the most favourable direction is the critical resolved shear stress:

For single crystals, slip occurs when φ = λ = 45°.
Defects in Crystal Structures
Crystals are never perfect – they are littered with defects that allow slip to occur at significantly lower values of applied stress than you would calculate from the equations above. There are three types of defects:
Point Defects – defects with atomic dimensions in all three directions, e.g. a missing atom (a vacancy)
Line Defects – defects in two atomic dimensions but are normal in the third direction.
Area Defects – defects in only one dimension, e.g. a grain boundary
All defects distort the lattice, increasing the energy stored inside it.
Line Defects
Line defects, also known as dislocations, is when a row of atoms is added or removed. These allow lattices to slip in steps, instead of all at once. Two types of dislocations are edge and screw dislocations:
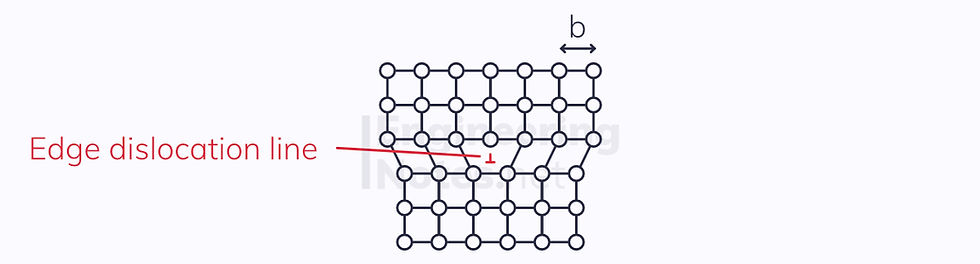
An edge dislocation is when a row of atoms is removed:
A screw dislocation is when a set of rows slips a certain amount to one side:
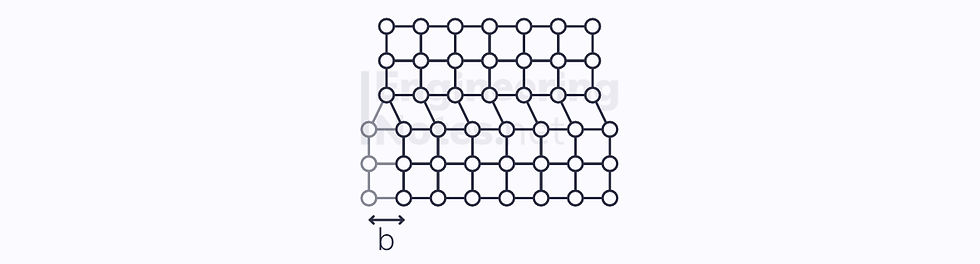
In both cases, the Burgers vector, b, measures the slip.
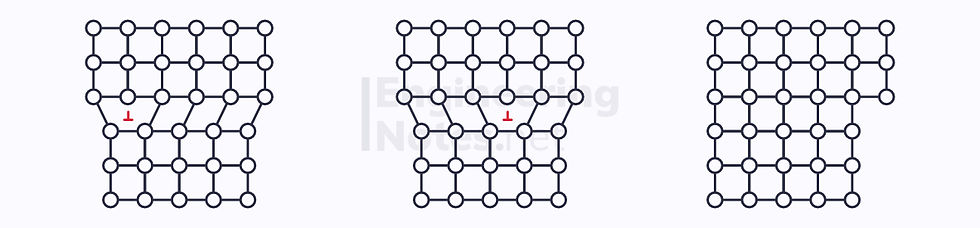
As you can see from this schematic, edge dislocations happen in steps, until the edge of the crystal has been reached and no more slip can occur. This is because far less energy is required to move only a small amount every time.
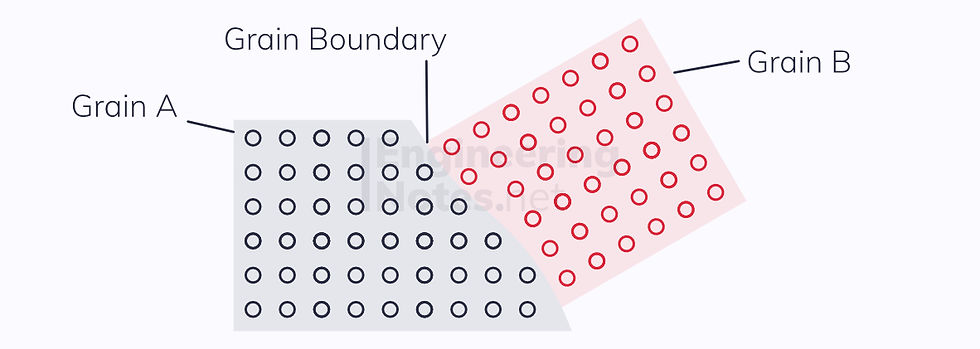
Area Defects & Grain Boundaries
Grain boundaries occur between uniform regions of crystal structures. These could be crystals of the same atom, or different. Either way, they provide a blockage to slip, as slip cannot occur across such a boundary.
A material with multiple crystal grains is known as a polycrystal.
The smaller the grains, the higher the stress required to cause slip. This is expressed by the Hall-Petch equation:
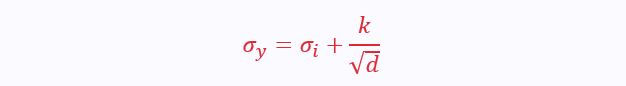
σ(y) is the yield strength
σ(i) is the intrinsic lattice strength
k is a material constant
d is the average diameter of grains
Strengthening
It may seem intuitive that more dislocations = less strong material, but this is not the case. Yes, a perfect material with no defects at all would be very strong, but this is impossible to achieve.
A small number of dislocations reduces the strength, but as you increase the number of dislocations, the strength actually increases. This is because the defects then interact and obstruct each other, reducing the likeliness of slip.
Therefore, the four main ways of strengthening a material are:
Reduce the grain size
Generate more dislocations
Adding smaller atoms into the lattice
Adding larger atoms into the lattice
The easiest methods of generating more dislocations to a structure are work hardening or melting and solidifying.
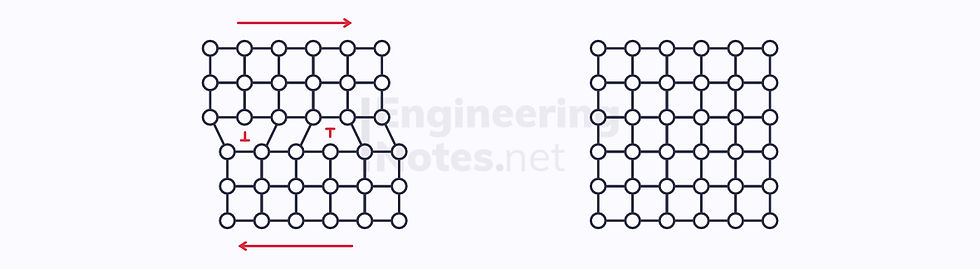
It is important to note, however, that you cannot add infinite dislocations to a structure. This is because two opposite dislocations will meet and annihilate:
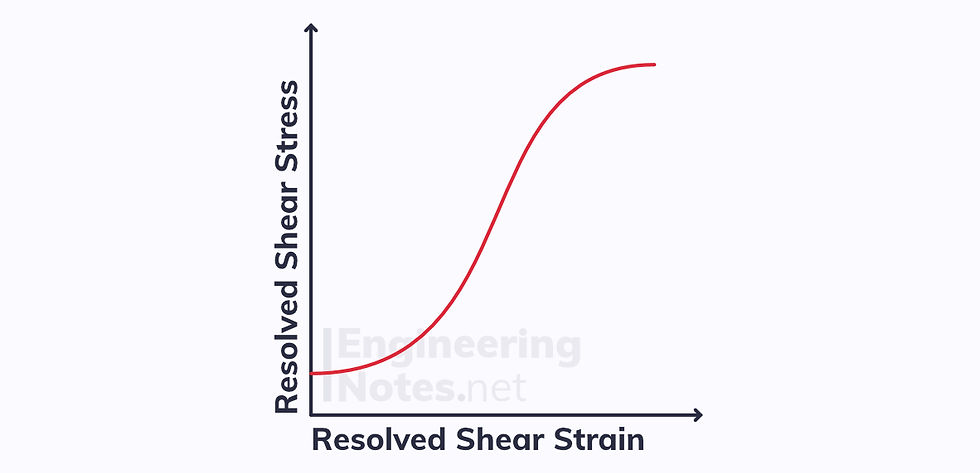
This leads to a resolved shear stress-strain curve like this:

Comments