Polar Coordinates

The Cartesian system in two-dimensions models points in terms of x and y. The polar system, however, models a point as a distance form the pole, r (generally the origin) at a certain angle from the initial line, θ (typically the positive horizontal axis). Yes, this is like the modulus-argument form of complex numbers and Argand diagrams.

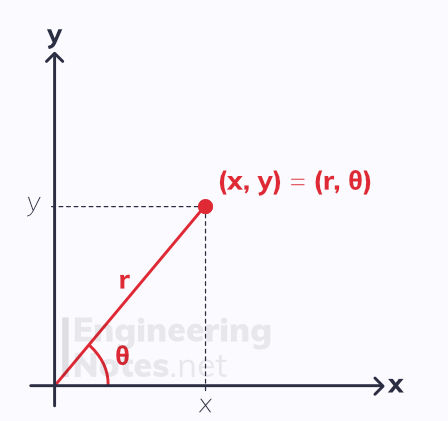
From the diagram, we can derive equations to convert between polar and Cartesian systems:

r cos(θ) = x

r sin(θ) = y

Where θ is given by:

θ = arctan(y/x)

And r is defined using Pythagoras' theorem:

r² = x² + y²

Sketching Polar Curves

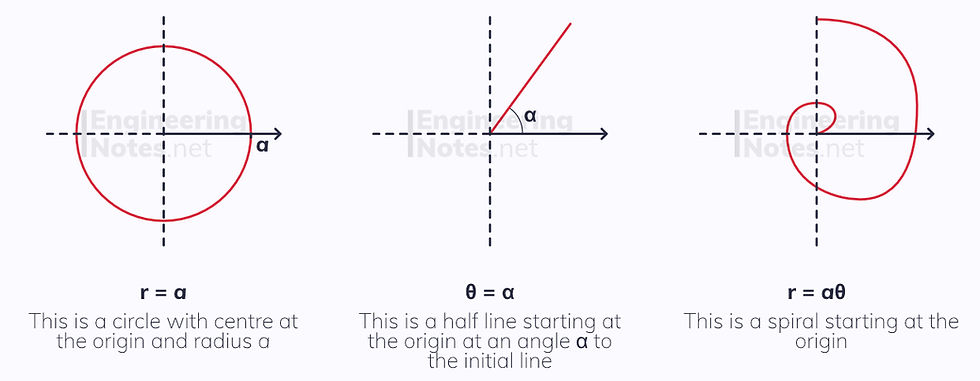
To sketch a polar curve, use a graphical calculator or draw u a table of values for regular intervals of θ. This can be done quickly using the table function on the CASIO ClassWiz fx-991EX, and we recommend using π/6 as an interval.

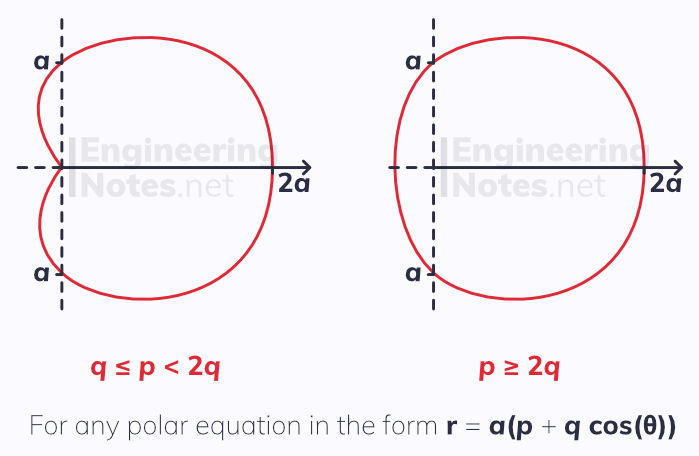
The curve in this example is known as a cardioid, due to its dimple. This is common for equations in the form r = a(p+qcos(θ)), but only if q ≤ p < 2q. When p ≥ 2q, there is no dimple, making it more egg-shaped:

Areas Enclosed by Polar Curves

The area of a sector of a polar curve can be calculated using integration. However, simply integrating r will not work. Instead:

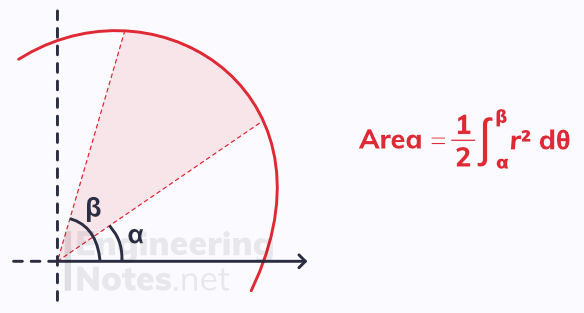
Of course, you an also calculate areas between polar curves. To do this, you need to find the angle at which they intersect.

Tangents to Polar Curves

To find tangents to a polar curve, you need to convert it into Cartesian form (one equation for x and one for y, both in terms of θ), using the formula at the top of this notes sheet. Then, you can differentiate parametrically.

Standard results are: