Acceleration, Projectiles & Kinematics

Velocity is the rate of change of an object's position, and therefore has direction. This makes it a vector quantity, unlike speed which is scalar (magnitude but no direction).

velocity = distance / time

The units of velocity are m/s

Acceleration is the rate of change of velocity, and so is the mathematical derivative of this.

acceleration = change in velocity / change in time

The units of acceleration are m/s²

Motion Graphs

We can plot motion on two main types of graph - it is important to know the properties of each.

Displacement-Time Graphs

• The Gradient is the velocity - draw a tangent to find the instantaneous velocity

• Horizontal line represents zero velocity

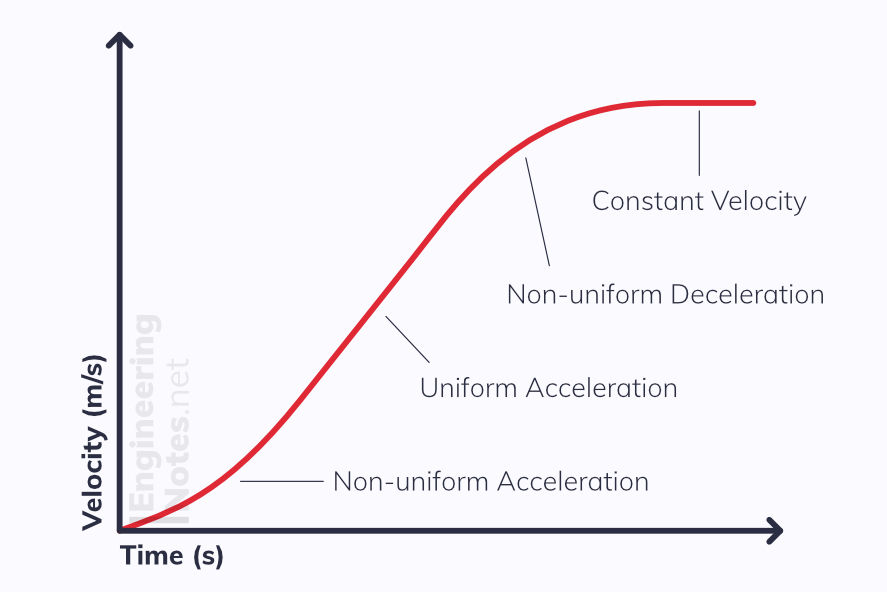
Velocity-Time Graphs

• The Gradient is the acceleration

• The Area beneath the graph is the displacement

Constant Acceleration

When acceleration is constant (e.g. free fall when we ignore air resistance), we can use SUVAT equations to work out the variables:

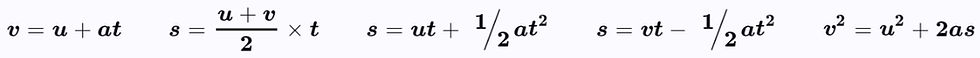
• s is for displacement

• u is for initial velocity

• v is for final velocity

• a is for acceleration

• t is for time

Vertical Motion due to Gravity

The gravitational force of the earth causes all objects to accelerate towards the ground, its surface. Ignoring air resistance, the acceleration is constant, and given a g:

g = 9.8 m/s²

This is independent of the mass, shape or velocity of the object.

It is vital to set a positive direction of motion for each question

In the example above, we set up as the positive direction, so our values for a and v were negative because the ball is going down.

Constant Acceleration with Vectors

Additionally, we can express motion using vectors:

r = r₀ + v t

• r is the position vector of the moving object

• r₀ is the initial position vector

• v is the velocity vector

Four of the five SUVAT equations have vector equivalents:

• v = u + at v = u + a t

• s = ut + ½at² s = u t + ½ a t² + r₀

• s = vt - ½at² s = v t - ½ a t² + r₀

• s = ½(u+v)t s = ½( u + v )t + r₀

v² = u² + 2as has no vector equivalent

Projectile Motion

When we model a projectile, we ignore air resistance. This means that:

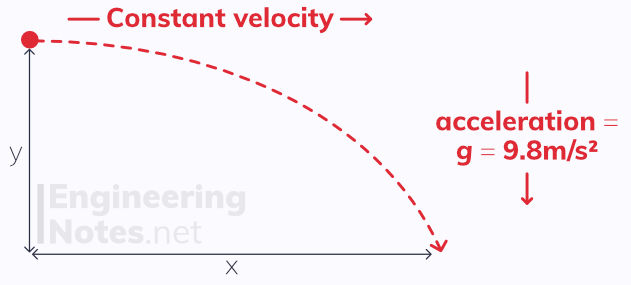
Horizontal motion of a projectile has constant velocity: a = 0

Vertical motion of a projectile motion is modelled as gravitational free fall: a = g

For horizontal projection, like in the diagram above:

• Since horizontal velocity is constant, we can use the equation x = vt (were x is horizontal displacement)

• For vertical velocity, we need to use SUVAT equations, due to the constant acceleration of g = 9.8 m/s²

Horizontal and Vertical Components

When given the velocity as a vector or at an angle, you must use trigonometry to find the vertical and horizontal components. Then, treat them separately as above (the horizontal component still has constant velocity)

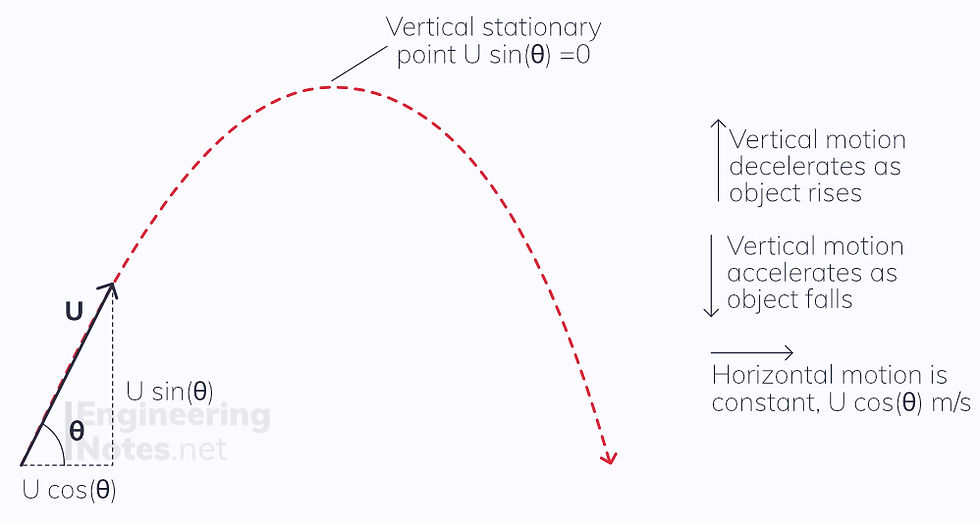
For an object projected at velocity U at an angle of θ to the x-axis:

• the horizontal component of the velocity is given as U cos(θ)

• the vertical component of the velocity is given as U sin(θ)

The vertical component is decelerating at -9.8 m/s² as it rises, and accelerates at 9.8 m/s² as it falls

The projectile reaches its maximum height when the vertical component of the velocity is zero.

Applying SUVAT to the vertical component of the projectile gives us a few standard and useful equations:

Projectile motion can also be plotted and calculated with in vectors.

Variable Acceleration

As you can see from the velocity-time graph, varying acceleration produces curves:

This is because the gradient of a velocity-time graph is the acceleration, and so if the acceleration changes with time, so must the gradient.

Kinematics

Velocity is the rate of change of displacement. Acceleration is the rate of change of velocity. Therefore:

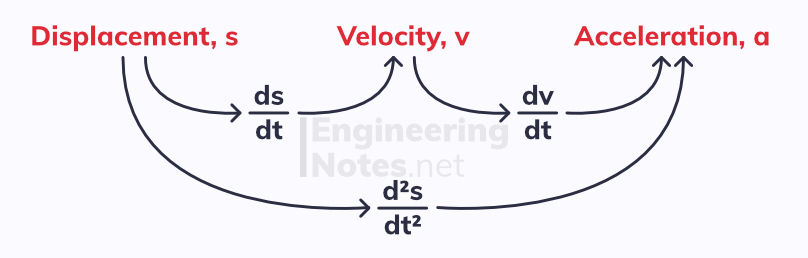
This means we can differentiate and integrate equations for motion:

Integrating and Differentiating Vectors

Variable acceleration can also be expressed in vector form. Therefore, you need to be able to differentiate and integrate vector equations.

Often, dot notation is used to quickly represent differentiation with respect to time:

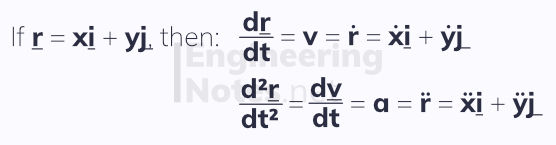
To integrate vectors:

In both differentiation and integration of vectors, you must do one term at a time

See Notes Sheets on differentiation and integration in Pure Maths if you need a recap.