top of page

Notes by Category University Engineering

Electronics*
Mathematics*
Mechanics & Stress Analysis*
Rate these notesNot a fanNot so goodGoodVery goodBrillRate these notes
Writer's pictureA-Level Maths
2 min read

Modelling in Mechanics

The real world of mechanics is incredibly complicated, with hundreds of different factors affecting motion and stability. This would be near impossible to calculate at this stage, so to simplify it we model objects and scenarios in a number of different ways.


Modelling Assumptions

Particle

  • Has negligible dimensions

  • Mass acts about a single point

  • Rotational forces and air resistance can be ignored

Rod

  • The diameter is negligible (so no thickness), only length counts

  • Mass acts along a line

  • It is rigid, so does not bend or buckle

Lamina

  • An object with only area, thickness is negligible (like a sheet of paper)

  • Mass acts across the flat surface

Uniform Body

  • The Mass is distributed evenly throughout the object

  • The mass is modelled to act through one point, the centre of mass, in the geometrical middle of the body

Light Object

  • The mass of the object is negligible

  • Often used for strings or pulleys

  • Allows us to model the tension on each end of a string as equal

Inextensible String

  • A string that does not stretch when a force is applied

  • Allows us to model the acceleration of two connected particles as the same

Smooth Surface

  • There is no friction between the surface and any object on it


Rough Surface

  • There is friction between the surface and any object on it

Wire

  • A rigid length of metal with negligible thickness (only modelled with length)

Smooth and Light Pulley

  • The pulley has no mass

  • No friction in the pulley, so tension is the same either side of it

Bead

  • A particle with a hole in it for string/wire to be threaded through

  • It can move freely along the wire or string

Peg

  • An object from which a body can be hung or rested

  • Modelled as dimensionless and fixed

  • Can be either rough or smooth

Air Resistance

  • Resistance forces due to motion through air

  • Almost always modelled as negligible

Gravity

  • The force of attraction between all objects

  • Acceleration due to gravity is given by g, which is 9.8 m/s² unless otherwise stated

  • Assume objects are always attracted to the ground (earth)

  • Gravity acts uniformly and downwards




Quantities & Units

Quantities can be either scalar or vector.

  • Scalar quantities have only magnitude

  • Vector quantities have both magnitude and direction


SI Base Units

Quantity Unit Symbol

Mass kilogram kg

Distance metre m

Time seconds s

Distance is scalar - the vector version of it is displacement

Derived Units

Quantity Unit Symbol

Velocity metres per second m/s

Acceleration metres per second² m/s²

Force Newtons N

Velocity is the vector form of speed, as velocity has direction as well as magnitude

Weight is not the same as mass. Weight is a force, measured in Newtons, N. It is given by:

W = mg Weight = mass x gravity



Representing Forces

Weight acts down from an object's centre of gravity. Other forces can act in any direction, and so to avoid confusion it is best to draw a force diagram:

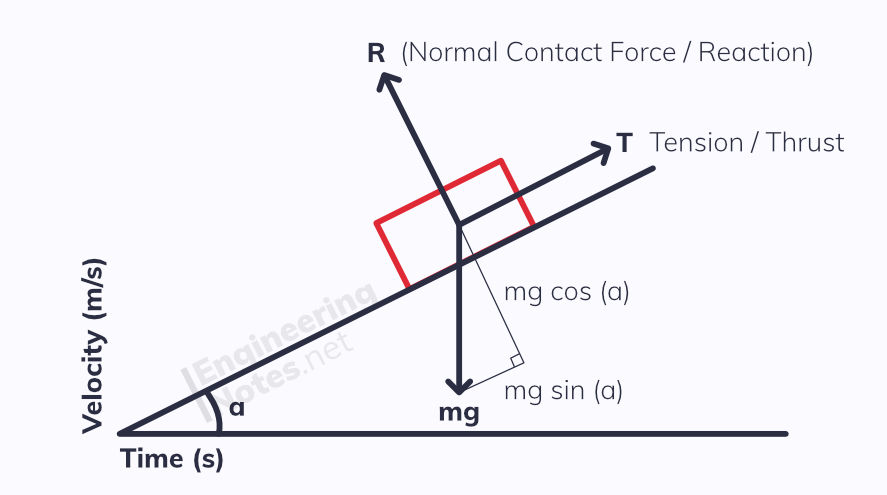
The length of arrow should represent the magnitude of the force. Single headed arrows represent forces.

If a system is in equilibrium - meaning there is no net resultant force and it is motionless or at constant velocity - then all the force arrows will make a closed shape. The example above would give a triangle.

Comments

bottom of page