Forces, Friction & Motion
- A-Level Maths

- Sep 9, 2020
- 3 min read
Updated: Dec 7, 2020
As seen in the Notes Sheet on Modelling in Mechanics, forces on an object can be expressed with a force diagram:

Newton's 1st Law:
On this diagram, you can see that T, the tension force pulling the object to the right, is equal to F, the friction between the the object and the surface - friction is the force that opposes motion.
This means that there is no resultant force to the left nor right, so the object remains motionless (it is in equilibrium). This is Newton's first law:
An object will stay at a constant velocity, or motionless, unless it experiences a resultant force.

Newton's 2nd Law:
Here, the surface is smooth (no friction). This means the object experiences a resultant force, T, to the right. According to Newton's second law, the resultant force on an object is directly proportional to the rate of change of momentum of the object, and acts in the same direction.
This is commonly expressed as:
F = ma Resultant Force = Mass x Acceleration (in direction of resultant force)

Newton's 3rd Law:
In this example, the object sits at rest on the surface with no horizontal forces acting on it. However, its weight, W, (mass x g) is a force acting down. If this were the only force, you would expect the object to accelerate down through the surface but it does not.
This means there is an equal but opposite force acting upwards: the normal reaction, R.
For every action, there is an equal but opposite reaction (equal in magnitude and type of force).

Forces in Two Dimensions
Often, forces will not be exactly horizontal or vertical. Instead, they may be given as vectors or at angles.

Sometimes you will need to find the resultant from two forces at right angles to one another, but more often you will be given the resultant and need to calculate the components. Use Pythagoras to do this.

When given the resultant at an angle, use trigonometry to find the components.

Moments
Moments are the turning forces acting on an object, around a pivot.
M = Fx moment = force × perpendicular distance from pivot
The units of moments are Nm
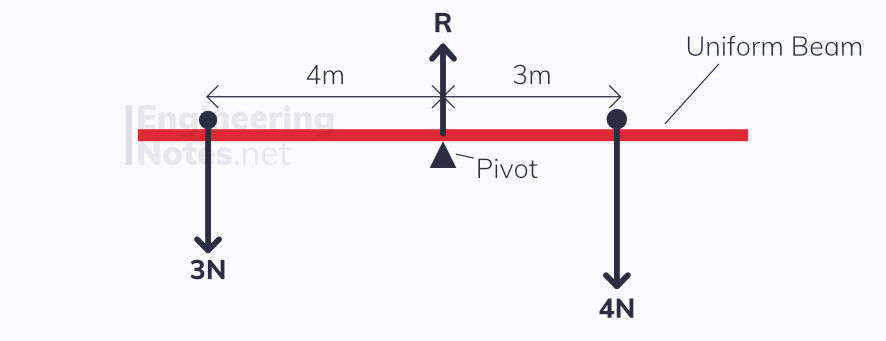
If there is a resultant moment in either direction (clockwise or anti-clockwise), then the object will rotate in that direction about its pivot.
When an object is in equilibrium, there is neither a net force nor a net moment in any direction. The Principle of moments can be used for this: the sum of all clockwise moments must equal the sum of all anticlockwise moments for an object to be in equilibrium.
When we model a rod or object as uniform, it means we assume all the weight is evenly distributed throughout, and only acts about the centre.
Tilting
The point of tilting is the point at which a rigid body is about to pivot.
When a rigid body is at the titling point, the reaction at any other support is zero.

Friction
Friction is the force that opposes motion. No materials are perfectly smooth, but have a degree of roughness: this is defined by the coefficient of friction, μ, which is a fixed property of a surface in certain conditions (conditions matter, because if a surface is wet, its coefficient of friction will be lower).
An object will only move on a surface if the force applied to it is greater than the maximum friction, F(max): this value is knows as the limiting value.

The limiting value, F(max), depends on both the normal reaction force, R, and the coefficient of friction, μ:
F(max) = μR Limiting Value = maximum friction = μR
Static Rigid Bodies
A rigid body is something like a rod or a ladder, leaning against a wall. If it is static, it is in equilibrium.
For a rigid body to be in equilibrium:
It must be stationary
There must be no resultant force in any direction
There must be no resultant moment
A common example is a ladder leaning against a wall, where there is friction on the ground:

Connected Particles & Pulleys

When the particles are moving along the same straight line, they can be modelled as one particle with a combined mass.

When the particles are moving separately, for example in a pulley system, they can be treated as separate particles.
In both instances, when the string is light and inextensible, the acceleration in each particle will be the same.
A common question will consist of two connected particles, one on an inclined plane, the other hanging off a pulley:




Comments