Motion, Momentum & Impulse
- A-Level Physics

- Jul 24, 2020
- 3 min read
Updated: Dec 7, 2020
Everything in the universe is in motion, and there are basic laws of mechanics that govern this.
Velocity is the rate of change of an object's position, and therefore has direction. This makes it a vector quantity, unlike speed which is scalar (magnitude but no direction).
velocity = distance / time
The units of velocity are m/s
Acceleration is the rate of change of velocity, and so is the mathematical derivative of this.
acceleration = change in velocity / change in time
The units of acceleration are m/s²
Motion Graphs
We can plot motion on two main types of graph - it is important to know the properties of each.

Displacement-Time Graphs
The Gradient is the velocity - draw a tangent to find the instantaneous velocity
Horizontal line represents zero velocity
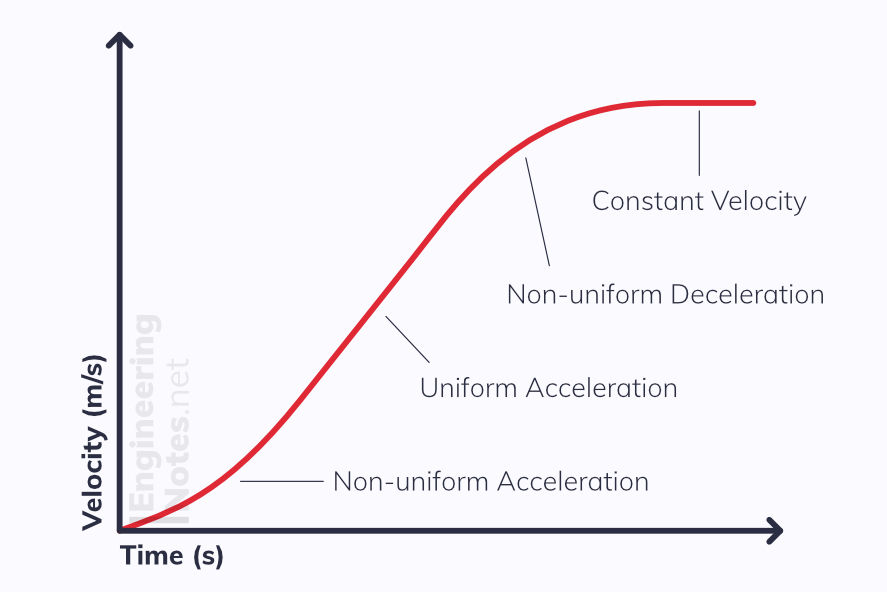
Velocity-Time Graphs
The Gradient is the acceleration
The Area beneath the graph is the displacement
Linear Motion
When acceleration is constant (e.g. free fall when we ignore air resistance), we can use SUVAT equations to work out the variables:
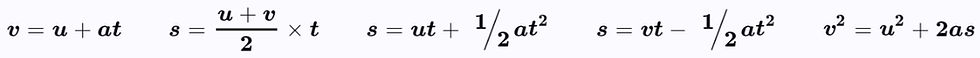
Linear motion can be investigated with trolley cars, air gliders, ticker tape, light gates, data loggers and motion capture.
Acceleration of free fall, g , should always be taken -9.81 unless otherwise stated. This can be looked at experimentally with electromagnetic trap doors triggering a timer, and light gates.
g = 9.81 m/s^2
Stopping Distance
Stopping distances are made up of thinking distance (the distance travelled in the time it takes the driver to react) and the braking distance (the distance travelled during the deceleration to standstill).
Projectile Motion
At A-Level, projectile motion is modelled as free fall - meaning air resistance is ignored. Of course, in reality, this is not the case (see Forces & Newton's Laws). Ignoring air resistance allows us to model the motion with constant acceleration, so we can use SUVAT, giving a neat, symmetrical curve:

In projectiles, it is important to split up horizontal and vertical components and to treat them as completely independent. Ignoring air resistance for both components, we can assume that horizontal velocity remains constant, whereas vertical velocity decelerates with gravity.
Momentum
For objects of changing acceleration or mass, using F = ma does not suffice. Therefore, momentum is used.
Momentum is a vector quantity (it has both magnitude and direction) dependent on the mass and velocity of an object.
p = mv momentum = mass x velocity
The units of momentum are kg m/s
Conservation of Momentum
When dealing with collisions in closed systems, you can use the principle of conservation of momentum to calculate the velocity of the objects before or after the collision. It is vital to establish a positive and negative direction, and not to get these confused, when doing collision calculations.
There are two types of collisions:
Perfectly Elastic Both momentum and kinetic energy are conserved
Inelastic Only momentum is conserved - kinetic energy is lost to other forms
It is important to note that in both collisions, the total energy is still conserved.
Impulse
In a collision, the resultant force on an object that causes the acceleration or deceleration changes dramatically over a very short period of time. This is very hard to analyse, and so we look at impulse instead.
Newton's Second Law tells us that the net force us equal to the rate of change of momentum.
Rearranging this gives
Change of momentum is equivalent to impulse
I = Ft Impulse = Force x time
The Units of Impulse are Newton Seconds, Ns, or kg m/s
Collisions can be plotted on force-time graphs, where the area under the line is the impulse.

Car Safety
If a car of mass 1000kg, travelling at 100km/h crashes into a wall and is brough to a stop, there is a very large change of momentum. If this happens quickly, a massive force is exerted on the car and driver. If this happens slowly, the same impulse will exert a far smaller force Think of it as flattening the curve - the area is the same, but shallower.
Therefore, cars are designed with 'crumple zones' to spread the impulse out as much as possible and minimise the force on the driver. The whole bonnet is deigned to be crushed, the seat belt is slightly elastic, and the airbags blow up in front of you, all to maximise the time taken for you to hurtle forward.



Comments