Quantum Physics

In 1900, Max Planck discovered that EM energy travelled in little packets rather than as a continuous wave (like charge, EM radiation is quantised - hence the name), suggesting EM radiation was, in fact, particulate. These little packets of energy are called photons. The photon model is used to explain how EM radiation interacts with matter, while the wave model explains its propagation through space.

The energy of a photon is directly proportional to its frequency:

E = hf energy = Planck′s constant × frequency

Planck’s Constant is 6.63 E−34

This can be combined with the wave equation for the speed of light in a vacuum:

E = hc/λ energy = Planck′s constant × 3.00 E8 / wavelength

Rearranging this shows that photon energy is inversely proportional to the wavelength.

Electron Volts

Because photon energy is so small (a red photon has an energy of 3.00 E-19 J), the electron volt, eV, is used. It is defined as the energy transferred to/from an electron when it moves through a p.d. of 1 Volt:

1 eV = 1.60 E−19 J

1 J = 6.25 E18 eV

Investigating Planck's Constant

Planck’s constant can be investigated by seeing at exactly what p.d. an LED goes on – the threshold voltage. This, multiplied by the elementary charge, gives the wave energy, and since we know the frequency of the light, we can deduce Planck’s Constant. Repeating this for a number of different colours will give a more accurate result.

The Photoelectric Effect

When UV radiation is shone onto certain metals, like zinc, electrons are released from the surface of the metal. These electrons are called photoelectrons, and a gold leaf electroscope can be used to demonstrate this occurring:

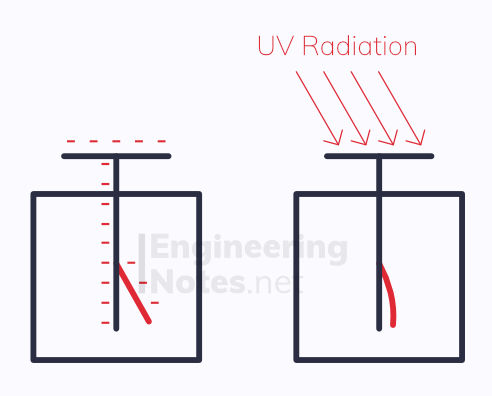
• The electroscope is given a negative charge, causing the gold leaf to stand erect (as like charges repel)

• UV light is shone onto the zinc plate

• If enough electrons are photoelectrons, the electroscope loses its charge and the gold leaf falls down

There are three key observations from the photoelectric effect:

1. Photoelectrons are only emitted if the UV radiation shining onto the zinc plate is above a certain frequency - this is called the threshold frequency. If the higher the frequency is above the threshold, the greater the kinetic energy of the emitted photoelectron.

2. If the radiation is above the threshold frequency, photoelectron emission is immediate and instantaneous - suggesting that it is brought about by one particle of radiation hitting the surface (a photon).

3. Increasing the intensity of the UV radiation does not increase the kinetic energy of the photoelectron emitted. Instead, increasing the intensity causes more photoelectrons to be emitted.

The Work Function

The threshold frequency is explained because an electron will only be emitted if the photon has enough energy to do so. The minimum energy for emission is the work function, ϕ:

Einstein's Photoelectric Equation

The energy transfer is explained in Einstein’s Photoelectric equation:

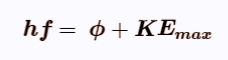
It is the maximum KE, because some electrons require more energy to be emitted than others, and as such will have less KE after they are emitted. This is because they are closer to the positive ions in the metal, and as such more energy is required to overcome the attraction between the electron and the positive metal ion.

The photoelectric equation can be re-written as the equation of a line, where Planck’s constant is the gradient and the work function the y-intercept.

Wave-Particle Duality

We have already established above that EM radiation, a wave, can have particle-like properties. This means that particles, like electrons, can also have wave-like properties...

Electron Diffraction

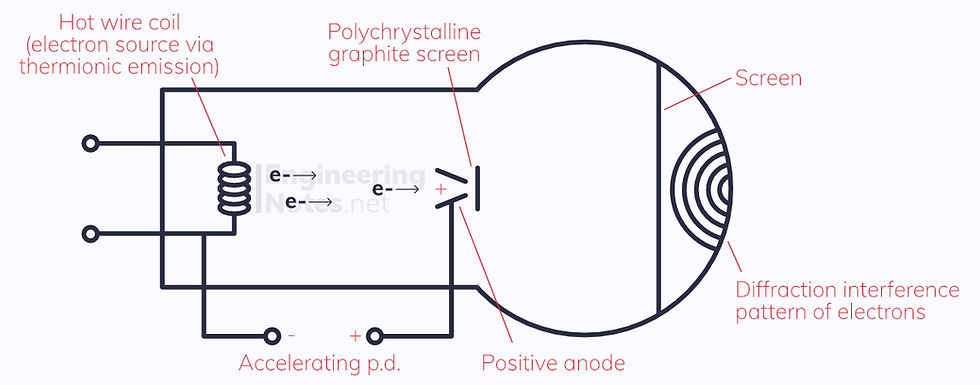
• Electrons are accelerated through a vacuum tube

• They collide with a polycrystalline graphite film

• The electrons pass through the spaces between the carbon atoms

• They fall onto a fluorescent screen, which shows a series of concentric circles where they land

This shows the polycrystalline carbon acts as a diffraction grating - the gaps in the carbon structure are roughly the size of the wavelength of the accelerated electrons.

The de Broglie wavelength

The smaller the voltage, the slower the electrons, the wider the gaps between rings – this shows the wavelength of a particle is inversely proportional to its momentum:

λ= h/p wavelength = Planck′s Constant / momentum

The larger a particle, the harder it is to observe its wave like properties, as its momentum is so large, giving it a minuscule wavelength. This is why it is generally only seen with electrons.