Exponentials and Logarithms

An exponential function is one a constant is raised to the power of a variable:

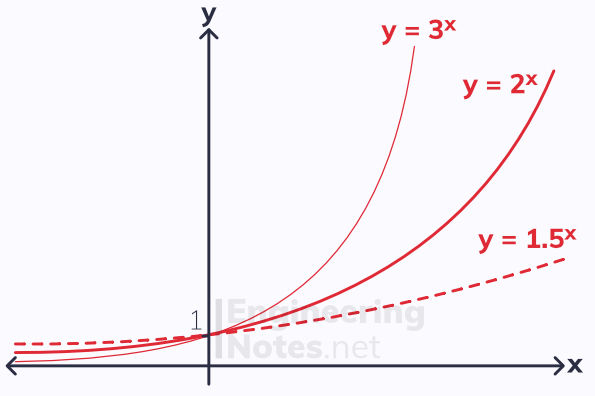
• The larger the coefficient, the steeper the graph

• All exponential functions in the form y = a^x pass through (0, 1)

• The value of the function decreases as x tends to 0

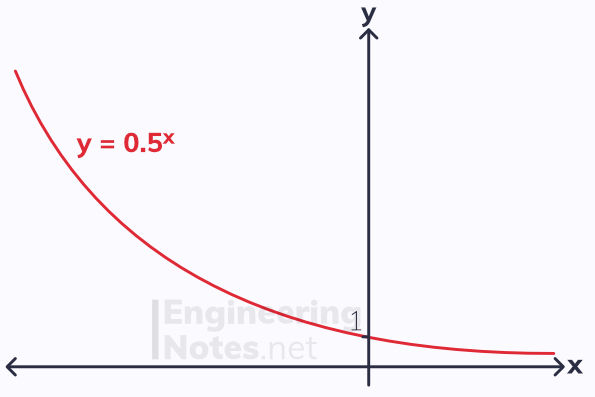
Functions in the form y = a^x where 0 < a < 1 are the other way around:

The gradient graphs of an exponential function are always very similar, but when a = 2.72 (e), the gradient graph is exactly the same:

For all real values of x:

if f(x) = e^x, f'(x) = e^x

if f(x) = e^kx, f'(x) = ke^kx

Functions in e can be used to model growth or decline where the rate of increase in number is proportional to the number.

Logarithms

Logarithms are the inverse of exponential functions.

Just as indices laws apply to exponentials, there are a series of laws that apply to logarithms - these are known as the log rules or laws of logarithms:

When working with difficult equations with exponents, it can be helpful to apply logarithms to both sides:

The Natural Logarithm, ln

The natural logarithm, ln, is the logarithm in base e. The graph of ln(x) is reflection of e^x in the line y=x:

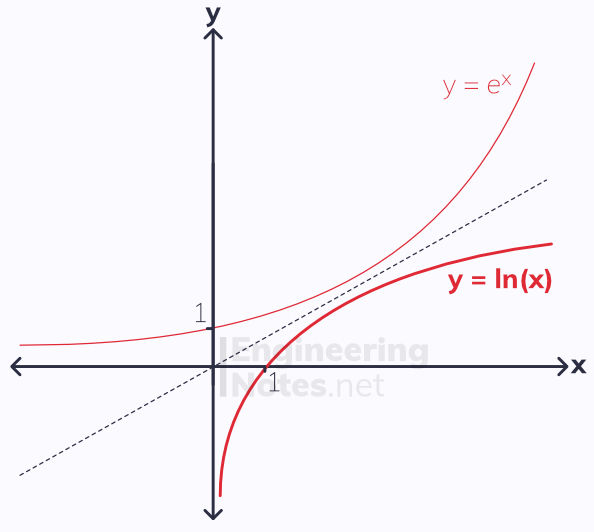
The y=axis is an asymptote in this graph, meaning that

ln(x) is only defined when x > 0

Logarithms and Non-Linear Data

Often, it is helpful to model non-linear data as linear. This can be achieved by taking logs of one or both sides of the equation:

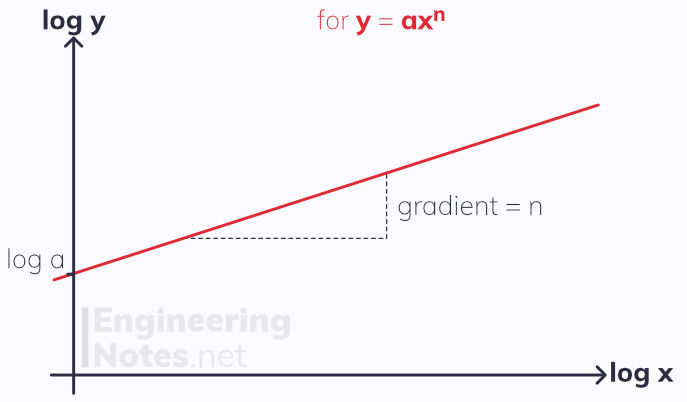
• If the equation is in the form y = ax^n, a graph of log y against log x will give a straight line where log a is the y intercept and n the gradient.

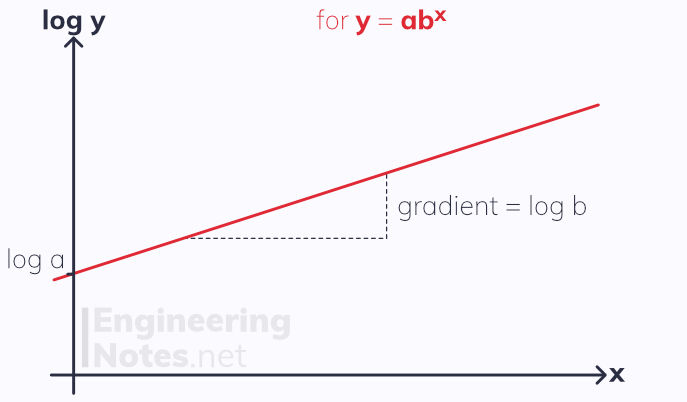
• If the equation is in the form y = ab^x, a graph of log y against x will give a straight line where log a is the y intercept and log b the gradient.