Quadratic & Simultaneous Equations and Inequalities

The standard format of a quadratic expression is ax² + bx + c

There are three ways of solving quadratic equations:

Factorising

Factorise a quadratic in the form ax² + bx + c = 0, and set each bracket to equal 0 to find the values of x (the roots).

The Quadratic Equation

The (b² - 4ac) inside the square root is known as the discriminant, and is used to show how many roots a quadratic has:

• b² - 4ac > 0: The quadratic has two distinct roots

• b² - 4ac = 0: The quadratic has one repeated root

• b² - 4ac < 0: The quadratic has no real roots

Completing the Square

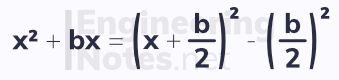
More commonly, quadratics are in their standard form. In this case, this version is used:

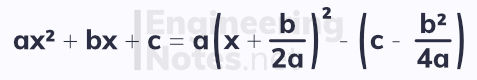
Simultaneous Equations

Linear Simultaneous Equations

There are two ways of solving linear simultaneous equations: elimination and substitution.

For example, solve the following simultaneous equations:

x + 3y = 11

4x - 5y = 10

Elimination

• Multiply the first equation by 4

  • 4x + 12y = 44

  • 4x - 5y = 10

• Subtract

  • 17y = 34

  • y = 2

• Substitute this into equation 1

  • x + 6 = 11

  • x = 5

Substitution

• Rearrange the first equation to make x the subject

  • x = 11 - 3y

• Substitute this into the second equation and solve

  • 4(11 - 3y) - 5y = 10

  • 44 - 12y - 5y = 10

  • 44 - 17y = 10

  • -17y = -34

  • y = 2

• Substitute this into the rearranged equation 1

  • x = 11 - 3(2)

  • x = 5

Quadratic Simultaneous Equations

Two simultaneous equations, one linear and one quadratic, can have up to two pairs of solutions. Don't get confused between the tow pairs!

You always use the substitution method above to solve quadratic simultaneous equations - rearrange the linear equation and sub into the quadratic:

Solve the simultaneous equations, x + 2y = 3, and x² +3xy = 10

• Rearrange linear equation to make x the subject

  • x = 3 - 2y

• Substitute into quadratic equation & solve

  • (3 - 2y)² + 3y(3 - 2y) = 10

  • 9 - 12y + 4y² + 9y - 6y² = 10

  • 9 - 3y - 2y² = 10

  • 2y² + 3y +1 = 0

  • (2y +1)(y +1) = 0

  • y = -1/2, -1

• Find the corresponding x values

  • x = 3 - 2(-1/2)

  • x = 4

  • x = 3 - 2(-1)

  • x = 5

• Get the pairs together correctly:

  • x = 4, y = -1/2 and x = 5, y = -1

Graphing Simultaneous Equations

The solutions to a pair of simultaneous equations represents the intersections between their graphs. For a linear and quadratic pair of simultaneous equations, you can use the discriminant of the substituted equation (the linear equation substituted into the quadratic equation) to show whether or not there are any solutions, and if so, how many.

Inequalities

There is certain notation for inequalities on a number line:

Linear inequalities are rearranged to make the variable the subject.

To solve a quadratic inequality:

• rearrange so that to the right of the inequality sign is 0

• solve the remaining quadratic on the left

• Sketch this equation roughly to see where the roots are and if it is positive or negative

• Identify the correct section.

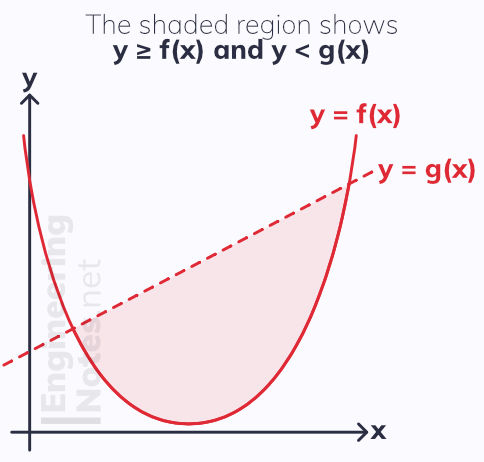
Regions on Graphs

It is possible to show regions closed off by one or multiple lines on a graph. Again, there is certain notation to be aware of:

• Dashed lines do not include the curve

• Solid lines do include the curve

• Shaded areas represent the defined region