The Binomial Expansion

Pascal's Triangle is used to expand binomial expressions like (a+b)ⁿ. It is created by summing adjacent pairs to find the number beneath this pair, starting from 1. Here are the first five rows:

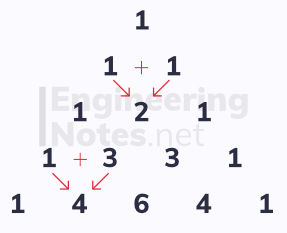
The (n + 1)th row of Pascal's triangle gives the coefficients in the expansion of (a+b)ⁿ

Factorial Notation

Parts of Pascal's triangle can be calculated quickly using factorial notation, ⁿCr (spoken "n choose r"):

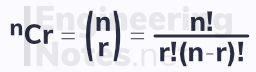
Expanding (a+b)ⁿ

When n ∈ ℕ (when n is a positive integer) the binomial expansion is in its simplest form:

The general term in an expansion of (a+b)ⁿ is given as:

Expanding (1+x)ⁿ

If n is a fraction or a negative number, you need to use this form of the binomial expansion:

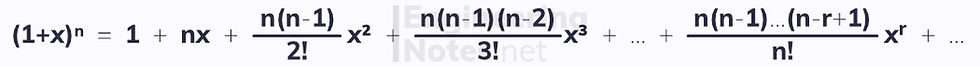
It is valid when |x| < 1 and when n ∈ ℝ

The general term in this expansion is given as:

x-term Coefficient

When the x term has a coefficient, so the binomial is in the form (1+bx)ⁿ, treat (bx) as x, and follow the standard expansion for (1+x)ⁿ

The expansion for (1+bx)ⁿ is valid for |bx| < 1, or |x| < 1/|b|

Double Coefficients

If the binomial is in the form (a+bx)ⁿ, you have to take a factor of aⁿ out of each term:

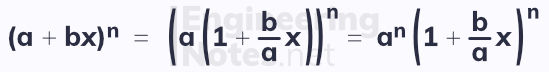
The expansion for (a+bx)ⁿ, where n is negative or a fraction, is valid when |bx/a| < 1, or |x| < |a/b|

• Often, complex expressions can be simplified first by splitting them into partial fractions (see notes sheet on algebraic methods), then by using a binomial expansion.